题目内容
4.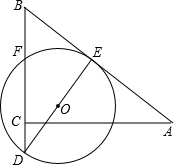 如图,△ABC中,AC=4,BC=3,∠ACB=90°,E、F分别为AB、BC的中点,⊙O经过E、F两点,点C在⊙O内,延长BC交⊙O于D.若∠BDO=∠A.
如图,△ABC中,AC=4,BC=3,∠ACB=90°,E、F分别为AB、BC的中点,⊙O经过E、F两点,点C在⊙O内,延长BC交⊙O于D.若∠BDO=∠A.(1)求证:AB为⊙O的切线;
(2)求点O到△ABC三边的距离各是多少?
分析 (1)欲证明AB为⊙O的切线,只需推知DE⊥AB即可;
(2)利用相似三角形△ABC∽△DBE、△ABC∽△DBE求得点O到AB的距离即可OE的长度;过O作OH⊥AC于点H,由面积法求得OH的长度.
解答 (1)证明:∵∠ACB=90°,
∴∠A+∠B=90°.
∵∠BDO=∠A,
∴∠B+∠BDO=90°,
∴DE⊥AB.
又DE是圆O的直径,
∴AB为⊙O的切线;
(2)解:∵在△ABC中,AC=4,BC=3,∠ACB=90°,
∴由勾股定理知,AB=5.
∵E为AB的中点,
∴BE=$\frac{1}{2}$AB=2.5.
由(1)知,DE⊥AB.
又∠BDO=∠A,
∴△ABC∽△DBE,
∴$\frac{DE}{AC}$=$\frac{BE}{BC}$,即$\frac{DE}{4}$=$\frac{2.5}{3}$,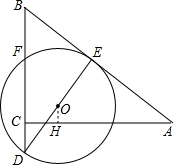
∴DE=$\frac{10}{3}$,
∴OE=$\frac{1}{2}$DE=$\frac{5}{3}$.
如图,过O作OH⊥AC于点H,
∵S△AOC+S△AOB+S△BOC=S△ABC,
∴$\frac{1}{2}$×4OH+$\frac{1}{2}$×5×$\frac{5}{3}$+$\frac{1}{2}$×3×1=$\frac{1}{2}$×3×4,
则OH=$\frac{1}{3}$,
∴点O到△ABC三边的距离各是:$\frac{5}{3}$、1、$\frac{1}{3}$.
点评 本题考查了切线的判定,相似三角形的判定与性质.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
12.在一条直线上依次有A,B,C三点,线段AB=3cm,线段BC=2cm,那么A,C两点间的距离是( )
| A. | 1cm | B. | 5cm | C. | 1cm或5cm | D. | 无法确定 |
14.随着n的值变大,代数式$1+\frac{1}{n}$的值变的越来越接近于( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是$\sqrt{3}$.
如图,四边形ABCD中,AB=AD,AD∥BC,∠ABC=60°,∠BCD=30°,BC=6,那么△ACD的面积是$\sqrt{3}$. 如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.
如图,在四边形ABCD中,AB=AD,AC与BD交于点E,∠ADB=∠ACB.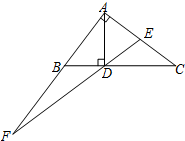 如图,△ABC中,∠BAC=90°,AD⊥BC于点D,点E为AC的中点,ED的延长线交AB的延长线于点F.若AB=5,BD=3,则$\frac{DF}{AF}$=$\frac{3}{4}$.
如图,△ABC中,∠BAC=90°,AD⊥BC于点D,点E为AC的中点,ED的延长线交AB的延长线于点F.若AB=5,BD=3,则$\frac{DF}{AF}$=$\frac{3}{4}$. 如图,点P(a,b)是直角坐标系中的一动点,O为坐标原点.
如图,点P(a,b)是直角坐标系中的一动点,O为坐标原点. 如图,△ABC中,AB=10,BC=8,AC=6,将△ABC折叠,使一边的两个端点重合,折痕为MN,求没有重合部分所成的三角形的周长.
如图,△ABC中,AB=10,BC=8,AC=6,将△ABC折叠,使一边的两个端点重合,折痕为MN,求没有重合部分所成的三角形的周长.