题目内容
20.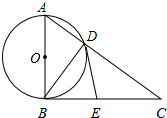 如图,已知Rt△ABC,∠ABC=90°,以直角边AB为直径作圆O,交斜边AC于点D,连结BD.
如图,已知Rt△ABC,∠ABC=90°,以直角边AB为直径作圆O,交斜边AC于点D,连结BD.(1)若AD=6,BD=8,求边BC的长;
(2)取BC的中点E,连结ED,试证明ED与⊙O相切.
分析 (1)由AB为圆O的直径,利用圆周角定理得到∠ADB为直角,在直角三角形ABD中,利用勾股定理求出AB的长,利用同角的余角相等得到一对角相等,再由公共角相等,利用两对角相等的三角形相似得到三角形ABD与三角形ACB相似,由相似得比例求出BC的长即可;
(2)连接OD,OE,利用直角三角形斜边上的中线等于斜边的一半得到DE=BE,利用SSS得到三角形OBE与三角形ODE全等,利用全等三角形的对应角相等得到∠ODE为直角,即可得证.
解答 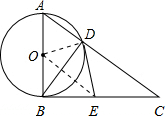 (1)解:∵AB为圆O的直径,
(1)解:∵AB为圆O的直径,
∴∠ADB=90°,
在Rt△ABD中,AD=6,BD=8,
根据勾股定理得:AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵∠ABD+∠DBC=90°,∠A+∠C=90°,
∴∠ABD=∠C,
∵∠A=∠A,
∴△ABD∽△ACB,
∴$\frac{AD}{AB}$=$\frac{BD}{BC}$,即$\frac{6}{10}$=$\frac{8}{BC}$,
解得:BC=$\frac{40}{3}$;
(2)证明:连接OD,OE,
在Rt△BDC中,E为BC的中点,
∴DE=BE=CE=$\frac{1}{2}$BC,
在△OEB和△OED中,
$\left\{\begin{array}{l}{OB=OD}\\{OE=OE}\\{BE=DE}\end{array}\right.$,
∴△OEB≌△OED(SSS),
∴∠ODE=∠OBE=90°,
则DE与圆O相切.
点评 此题考查了切线的判定,相似三角形的判定与性质,勾股定理,圆周角定理,以及直角三角形斜边上的中线性质,熟练掌握切线的判定方法是解本题的关键.

练习册系列答案
相关题目
11.计算(-a3)2+(-a2)3的结果为( )
| A. | -2a6 | B. | -2a5 | C. | 2a6 | D. | 0 |
8.若∠α与∠β同旁内角,且∠α=50°时,则∠β的度数为( )
| A. | 50° | B. | 130° | C. | 50°或130° | D. | 无法确定 |
 如图是七年级(1)班学生参加课外兴趣小组人数的扇形统计图.如果参加外语兴趣小组的人数是12人,那么参加绘画兴趣小组的人是5人.
如图是七年级(1)班学生参加课外兴趣小组人数的扇形统计图.如果参加外语兴趣小组的人数是12人,那么参加绘画兴趣小组的人是5人.
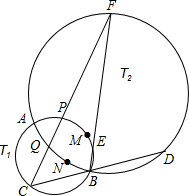 如图,两圆T1、T2相交于A、B两点,过点B的一条直线分别交圆T1、T2于点C、D,过点B的另一条直线分别交圆T1、T2于点E、F,直线CF分别交圆T1、T2于点P、Q,设M、N分别是弧PB、弧QB的中点,求证:若CD=EF,则C、F、M、N四点共圆.
如图,两圆T1、T2相交于A、B两点,过点B的一条直线分别交圆T1、T2于点C、D,过点B的另一条直线分别交圆T1、T2于点E、F,直线CF分别交圆T1、T2于点P、Q,设M、N分别是弧PB、弧QB的中点,求证:若CD=EF,则C、F、M、N四点共圆.