Question

17．在△ABC中，∠C=90°，cosA=$\frac{4}{5}$，则sinA=$\frac{3}{5}$tanB=$\frac{4}{3}$．

Answer 1

分析 根据已知设设AC=4x，AB=5x，由勾股定理求出BC=3x，根据锐角三角函数的定义求出即可．

解答 解：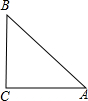
∵在△ABC中，∠C=90°，cosA=$\frac{4}{5}$=$\frac{AC}{AB}$，
∴设AC=4x，AB=5x，由勾股定理得：BC=3x，
∴sinA=$\frac{BC}{AB}$=$\frac{3x}{5x}$=$\frac{3}{5}$，tanB=$\frac{AC}{BC}$=$\frac{4x}{3x}$=$\frac{4}{3}$，
故答案为：$\frac{3}{5}$，$\frac{4}{3}$．

点评 本题考查了锐角三角函数的定义，同角三角函数的关系的应用，能熟记锐角三角函数的定义是解此题的关键．