题目内容
12.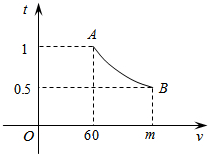 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=$\frac{k}{v}$其图象为如图所示的一段曲线且端点为A(60,1),和B(m,0.5)
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=$\frac{k}{v}$其图象为如图所示的一段曲线且端点为A(60,1),和B(m,0.5)(1)求k和m的值.
(2)若行驶速度不得超过80km/h,则汽车通过该路段最少需要多少时间.
分析 (1)把A代入解析式,利用待定系数法求得函数解析式,然后把(m,0.5)代入解析式求得m的值;
(2)求得当v=80时t的值,根据图象即可作出解答.
解答 解:(1)把A(60,1)代入t=$\frac{k}{v}$得$\frac{k}{60}=1$,解得:k=60,
则反比例函数的解析式是t=$\frac{60}{v}$,把(m,0.5)代入得m=120;
(2)把v=80代入解析式t=$\frac{60}{80}$=$\frac{3}{4}$,
则当汽车通过该段路段的时间最少是$\frac{3}{4}$h.
点评 本题考查了反比例函数的实际应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.下列各数中,数值相等的是( )
| A. | 32和23 | B. | -23和(-2)3 | C. | -32和(-3)2 | D. | -(-3)和-|-3| |
7.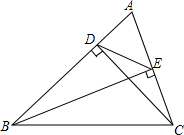 如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )
如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )
 如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )
如图,△ABC中,CD⊥AB于点D,BE⊥AC于点E,连接DE,AD=2,AB=9,AC=6,下列说法正确的是( )| A. | AE=3 | B. | BE=$\frac{1}{3}$$\sqrt{713}$ | C. | CE=$\frac{14}{3}$ | D. | DE=2 |
4.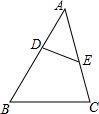 如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )
如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )
 如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )
如图,在△ABC中,点D,E分别是AB,AC边上的两个点,且$\frac{AE}{AB}=\frac{AD}{AC}=\frac{1}{2}$,则S△ADE:S△ABC的值为( )| A. | 1:$\sqrt{3}$ | B. | 1:2 | C. | 1:3 | D. | 1:4 |
1.下列多项式中是二次三项式的是( )
| A. | a+3b | B. | a2+2a+1 | C. | 3a+4ab2+5b | D. | a3+b3 |
 如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.
如图,长方形ABCD中,AB=9,AD=4.E为CD边上一点,CE=6.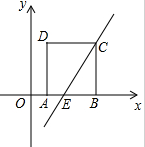 如图,正方形ABCD的边长是4,将此正方形置于平面直角坐标系中,使AB在x轴正半轴上,A点的坐标是(1,0),经过点C的直线y=$\frac{3}{4}$x+b与x轴交于点E,与y轴交于点F.
如图,正方形ABCD的边长是4,将此正方形置于平面直角坐标系中,使AB在x轴正半轴上,A点的坐标是(1,0),经过点C的直线y=$\frac{3}{4}$x+b与x轴交于点E,与y轴交于点F.