题目内容
2.化简:$\sqrt{(1-\frac{π}{2})^{2}}$-$\sqrt{(π-3)^{2}}$=-$\frac{π}{2}+2$.分析 根据二次根式的性质的可知,一个数的算术平方根是非负数,从而解答本题.
解答 解:∵$1-\frac{π}{2}<0$
∴$\sqrt{(1-\frac{π}{2})^{2}}=\frac{π}{2}-1$
又∵π-3>0
∴$\sqrt{(π-3)^{2}}=π-3$
∴$\sqrt{(1-\frac{π}{2})^{2}}-\sqrt{(π-3)^{2}}$
=$(\frac{π}{2}-1)-(π-3)$
=$\frac{π}{2}-1-π+3$
=$-\frac{π}{2}+2$.
点评 本题考查二次根式的性质和化简,关键是判断根号内是正数的平方还是负数的平方.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
12.在一条直线上依次有A,B,C三点,线段AB=3cm,线段BC=2cm,那么A,C两点间的距离是( )
| A. | 1cm | B. | 5cm | C. | 1cm或5cm | D. | 无法确定 |
14.随着n的值变大,代数式$1+\frac{1}{n}$的值变的越来越接近于( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 在等边三角形ABC,DE∥AB,DE与边AB、AC分别交于D、E,△ADE是等边三角形吗?试说明理由.
在等边三角形ABC,DE∥AB,DE与边AB、AC分别交于D、E,△ADE是等边三角形吗?试说明理由.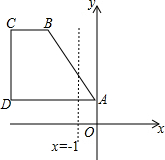 如图,已知四个点A(0,1),B(-3,4),C(-5,4),D(-5,1).
如图,已知四个点A(0,1),B(-3,4),C(-5,4),D(-5,1). 如图,已知AC=6cm,BC=9cm,∠B=30°,∠D=115°,△ABC∽△DAC,
如图,已知AC=6cm,BC=9cm,∠B=30°,∠D=115°,△ABC∽△DAC,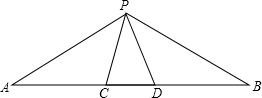 如图,点C,D在线段AB上,P是直线AB外一点,连接PA,PB,PC,PD.已知△PCD是等边三角形,如果CD2=AC•DB,求∠APB的度数.
如图,点C,D在线段AB上,P是直线AB外一点,连接PA,PB,PC,PD.已知△PCD是等边三角形,如果CD2=AC•DB,求∠APB的度数.