题目内容
在长8cm,宽6cm的矩形中,截去一个矩形,使留下的矩形与原矩形相似,那么留下的矩形面积是 cm2.
考点:相似多边形的性质
专题:
分析:由题意,在长为8cm宽6cm的矩形中,截去一个矩形使留下的矩形与原矩形相似,根据相似形的对应边长比例关系,就可以求解.
解答:解:设宽为x,
∵留下的矩形与原矩形相似,
∴
=
,
解得x=
.
∴截去的矩形的面积为
×6=21cm2,
∴留下的矩形的面积为48-21=27cm2,
故答案为:27.
∵留下的矩形与原矩形相似,
∴
| 8-x |
| 6 |
| 6 |
| 8 |
解得x=
| 7 |
| 2 |
∴截去的矩形的面积为
| 7 |
| 2 |
∴留下的矩形的面积为48-21=27cm2,
故答案为:27.
点评:此题主要考查多边形相似的性质:对应边长成比例,相似比的平方等于面积比,学生对此性质要熟练掌握.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
过A、B、C三点,最多可确定直线的条数是( )
| A、1条 | B、3条 |
| C、1条或2条 | D、1条或3条 |
若
是方程组
的解,则a+b的值是( )
|
|
| A、2 | B、-2 | C、1 | D、-1 |
 直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则
直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则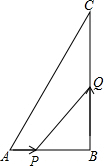 如图△ABC中,AB=6cm,BC=12cm,∠B=90°,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,那么经过几秒时,
如图△ABC中,AB=6cm,BC=12cm,∠B=90°,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,那么经过几秒时,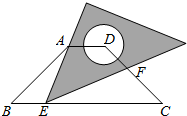 如图,在等腰梯形ABCD中,AD∥BC,BC=4
如图,在等腰梯形ABCD中,AD∥BC,BC=4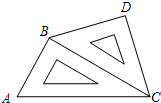 如图所示,把一副直角三角板摆放在一起,∠ACB=30°,∠BCD=45°,∠ABC=∠BDC=90°,量得CD=20CM,试求BC、AC的长.
如图所示,把一副直角三角板摆放在一起,∠ACB=30°,∠BCD=45°,∠ABC=∠BDC=90°,量得CD=20CM,试求BC、AC的长. 如图,AC=BD,要证△ABC≌△DCB,只需要增加一个条件是
如图,AC=BD,要证△ABC≌△DCB,只需要增加一个条件是