题目内容
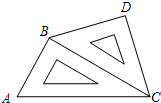 如图所示,把一副直角三角板摆放在一起,∠ACB=30°,∠BCD=45°,∠ABC=∠BDC=90°,量得CD=20CM,试求BC、AC的长.
如图所示,把一副直角三角板摆放在一起,∠ACB=30°,∠BCD=45°,∠ABC=∠BDC=90°,量得CD=20CM,试求BC、AC的长.考点:勾股定理
专题:
分析:在直角△BCD中,利用勾股定理求得BC的长度;然后在直角△ABC中由“30度角所对的直角边等于斜边的一半”和勾股定理来求AB的长度,则AC=2AB.
解答: 解:∵BD=CD=20,
解:∵BD=CD=20,
∴BC=
=
=20
(cm)
设AB=x,在Rt△ABC中,∵∠ACB=30°,则AC=2x.
∵由勾股定理得 AB2+BC2=AC2,
∴x2+(20
)2=(2x)2,
得x2=
,又x>0,
∴x=
,
即AC=2AB=
.
 解:∵BD=CD=20,
解:∵BD=CD=20,∴BC=
| BD2+CD2 |
| 202+202 |
| 2 |
设AB=x,在Rt△ABC中,∵∠ACB=30°,则AC=2x.
∵由勾股定理得 AB2+BC2=AC2,
∴x2+(20
| 2 |
得x2=
| 800 |
| 3 |
∴x=
20
| ||
| 3 |
即AC=2AB=
| 40 |
| 3 |
| 6 |
点评:本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,△ABC是等边三角形,AE⊥BC于E,AD⊥CD于D,AB∥CD,则图中60°的角有( )
如图,△ABC是等边三角形,AE⊥BC于E,AD⊥CD于D,AB∥CD,则图中60°的角有( )| A、3个 | B、4个 | C、5个 | D、6个 |
一种零件的长度在图纸上标为:10
(单位:mm),从一名工人生产的一批零件中抽出了四件,测出的长度如下,不合格的是( )
| 0 | +3 -5 |
| A、100mm | B、98mm |
| C、104mm | D、96mm |
 如图所示,边长为5的正方形ABCD的对角线相交于点O,过点O的直线EF分别交AD,BC于点E,F,则阴影部分的面积是
如图所示,边长为5的正方形ABCD的对角线相交于点O,过点O的直线EF分别交AD,BC于点E,F,则阴影部分的面积是 分析探索题:细心观察如图,认真分析各式,然后解答问题.
分析探索题:细心观察如图,认真分析各式,然后解答问题.