题目内容
 直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则
直角三角形纸片的两直角边长分别为6,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则| CE |
| BC |
考点:翻折变换(折叠问题)
专题:
分析:根据翻折的性质可得BE=AE,设CE=x,表示出BE,再利用勾股定理列方程求出x,然后相比计算即可得解.
解答:解:∵△ABC折叠后点A与点B重合,
∴BE=AE,
设CE=x,则BE=8-x,
在Rt△BCE中,BC2+CE2=BE2,
即62+x2=(8-x)2,
解得x=
,
所以
=
=
.
故答案为:
.
∴BE=AE,
设CE=x,则BE=8-x,
在Rt△BCE中,BC2+CE2=BE2,
即62+x2=(8-x)2,
解得x=
| 7 |
| 4 |
所以
| CE |
| BC |
| ||
| 6 |
| 7 |
| 24 |
故答案为:
| 7 |
| 24 |
点评:本题考查了翻折变换的性质,熟记翻折前后的图形能够互相重合得到相等的线段并利用勾股定理列出方程是解题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
正方形具有而菱形不具有的性质是( )
| A、对角线平分一组对角 |
| B、对角线相等 |
| C、对角线互相垂直平分 |
| D、四条边相等 |
下列判断中正确的是( )
| A、全等三角形是面积相等的三角形 |
| B、面积相等的三角形都是全等的三角形 |
| C、等边三角形都是面积相等的三角形 |
| D、面积相等斜边相等的直角三角形都是全等直角三角形 |
 如图,已知AF=BE,∠A=∠B,AC=BD,经分析
如图,已知AF=BE,∠A=∠B,AC=BD,经分析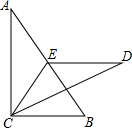 如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CE将△CBA折叠,使点A落在点D处,若CD恰好与EB垂直,则tanB的值为( )
如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CE将△CBA折叠,使点A落在点D处,若CD恰好与EB垂直,则tanB的值为( ) 如图所示,边长为5的正方形ABCD的对角线相交于点O,过点O的直线EF分别交AD,BC于点E,F,则阴影部分的面积是
如图所示,边长为5的正方形ABCD的对角线相交于点O,过点O的直线EF分别交AD,BC于点E,F,则阴影部分的面积是