题目内容
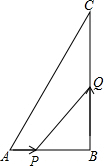 如图△ABC中,AB=6cm,BC=12cm,∠B=90°,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,那么经过几秒时,
如图△ABC中,AB=6cm,BC=12cm,∠B=90°,点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,那么经过几秒时,(1)△PBQ的面积等于8cm2?
(2)四边形APQC的面积最小?最小值是多少?
考点:一元二次方程的应用,二次函数的应用
专题:几何动点问题
分析:(1)根据直角三角形的面积公式和路程=速度×时间进行求解即可;
(2)四边形APQC的面积=△ABC的面积-△PBQ的面积,再根据配方法即可求解.
(2)四边形APQC的面积=△ABC的面积-△PBQ的面积,再根据配方法即可求解.
解答:解:(1)设x秒钟后,△PBQ的面积等于8cm2,由题意可得:
2x(6-x)÷2=8
解得x1=2,x2=4.
经检验均是原方程的解.
答:故经过2或4秒钟时,△PBQ的面积等于8cm2.
(2)依题意有:
12×6÷2-2x(6-x)÷2
=36-6x+x2
=(x-3)2+27,
故经过3秒时,四边形APQC的面积最小,最小值是27cm2.
2x(6-x)÷2=8
解得x1=2,x2=4.
经检验均是原方程的解.
答:故经过2或4秒钟时,△PBQ的面积等于8cm2.
(2)依题意有:
12×6÷2-2x(6-x)÷2
=36-6x+x2
=(x-3)2+27,
故经过3秒时,四边形APQC的面积最小,最小值是27cm2.
点评:此题主要考查了一元二次方程的应用,找到关键描述语“△PBQ的面积等于8cm2”,得出等量关系是解决问题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
正方形具有而菱形不具有的性质是( )
| A、对角线平分一组对角 |
| B、对角线相等 |
| C、对角线互相垂直平分 |
| D、四条边相等 |
下列判断中正确的是( )
| A、全等三角形是面积相等的三角形 |
| B、面积相等的三角形都是全等的三角形 |
| C、等边三角形都是面积相等的三角形 |
| D、面积相等斜边相等的直角三角形都是全等直角三角形 |
下列二次根式中与
是同类二次根式的是( )
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,AB∥CD,AD、BC相交于点O,若OA=2,OD=4,AB=3.
如图,AB∥CD,AD、BC相交于点O,若OA=2,OD=4,AB=3.