题目内容
17.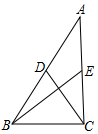 如图,在△ABC中,AB=9,AC=7,BE、CD为中线,且BE⊥CD,则BC=$\sqrt{26}$.
如图,在△ABC中,AB=9,AC=7,BE、CD为中线,且BE⊥CD,则BC=$\sqrt{26}$.
分析 设BE、CD交于点O,设OE=x,OB=2x,OD=y,OC=2y.构建方程组,求出x2+y2即可解决问题.
解答 解:设BE、CD交于点O,设OE=x,OB=2x,OD=y,OC=2y.
∵AD=BD=$\frac{9}{2}$,AE=CE=$\frac{7}{2}$,
∵BE⊥CD,
∴∠BOD=∠COE=90°,
∴$\left\{\begin{array}{l}{{y}^{2}+(2x)^{2}=(\frac{9}{2})^{2}}\\{{x}^{2}+(2y)^{2}=(\frac{7}{2})^{2}}\end{array}\right.$,
可得x2+y2=$\frac{13}{2}$,
∴BC=$\sqrt{(2x)^{2}+(2y)^{2}}$=$\sqrt{26}$.
故答案为$\sqrt{26}$.
点评 本题考查勾股定理、二元二次方程组、三角形的中线等知识,解题的关键是学会设未知数,构建方程组解决问题,学会用整体的思想思考问题,属于中考常考题型.

练习册系列答案
相关题目
7.下列水平放置的几何体中,俯视图是矩形的是( )
| A. |  | B. |  | C. |  | D. |  |
8.关于x的方程$\frac{1}{2x}$=$\frac{k}{x+3}$无解,则k的值为( )
| A. | 0或$\frac{1}{2}$ | B. | -1 | C. | -2 | D. | -3 |
12.下列命题是真命题的是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角线互相垂直的四边形是正方形 | |
| C. | 一组对边平行的四边形是平行四边形 | |
| D. | 四边相等的四边形是菱形 |
2.某商场为了迎接“6.1儿童节“,以调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如表:
当这些玩具调整后的单价都大于2元时,解答下列问题:
(1)y与x的函数关系式为,x的取值范围为;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了元;
(3)这n个玩具调整前、后的平均单价分别为$\overline{x}$(元)、$\overline{y}$(元),猜想$\overline{y}$与$\overline{x}$的关系式,并写出推导过程.
| 第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
| 调整前单价x (元) | x1 | x2=6 | x3=72 | x4 | … | xn |
| 调整后单价y (元) | y1 | y2=4 | y3=59 | y4 | … | yn |
(1)y与x的函数关系式为,x的取值范围为;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了元;
(3)这n个玩具调整前、后的平均单价分别为$\overline{x}$(元)、$\overline{y}$(元),猜想$\overline{y}$与$\overline{x}$的关系式,并写出推导过程.
6. 如图,AB∥CD,AD与BC相交于点E,若∠A=40°,∠C=35°,则∠BED=( )
如图,AB∥CD,AD与BC相交于点E,若∠A=40°,∠C=35°,则∠BED=( )
 如图,AB∥CD,AD与BC相交于点E,若∠A=40°,∠C=35°,则∠BED=( )
如图,AB∥CD,AD与BC相交于点E,若∠A=40°,∠C=35°,则∠BED=( )| A. | 70° | B. | 75° | C. | 80° | D. | 85° |
 如图,∠AOB=90°,∠BOC=30°,则∠AOC=60度.
如图,∠AOB=90°,∠BOC=30°,则∠AOC=60度.