题目内容
1.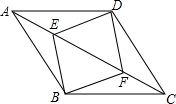 如图,E,F是菱形ABCD对角线上的两点,且AE=CF.
如图,E,F是菱形ABCD对角线上的两点,且AE=CF.(1)求证:四边形BEDF是菱形;
(2)若∠DAB=60°,AD=6,AE=DE,求菱形BEDF的周长.
分析 (1)连接BD,由菱形ABCD的性质得出OA=OC,OB=OD,AC⊥BD,得出OE=OF,证出四边形BEDF是平行四边形,再由EF⊥BD,即可证出四边形BEDF是菱形;
(2)求出∠DAE=30°,得出OD=$\frac{1}{2}$AD=3,再证出∠ADE=∠EDO=30°,在Rt△DEO中,由三角函数求出DE=$\frac{OD}{cos30°}$=2$\sqrt{3}$,即可得出菱形BEDF的周长.
解答 (1)证明:连接BD,交AC于O,如图所示: ∵四边形ABCD是菱形,
∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD,
∵AE=CF,
∴OE=OF,
∴四边形BEDF是平行四边形,
∵EF⊥BD,
∴四边形BEDF是菱形;
(2)解:∵∠DAB=60°,
∴∠DAE=30°,∠ADB=60°,
∵AD=6,
∴OD=$\frac{1}{2}$AD=3,
∵AE=DE,
∴∠DAE=∠ADE,∠ADE=∠EDO=30°,
在Rt△DEO中,DE=$\frac{OD}{cos30°}$=2$\sqrt{3}$,
∴菱形BEDF的周长=4DE=8$\sqrt{3}$.
点评 本题考查了菱形的性质与判定、平行四边形的判定、等腰三角形的性质以及三角函数的运用;熟练掌握菱形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
11.用换元法解方程$\frac{y}{{y}^{2}-3}$+$\frac{{y}^{2}-3}{y}$=$\frac{5}{2}$时,如果设x=$\frac{y}{{y}^{2}-3}$,那么原方程可化为( )
| A. | 2x2-5x+2=0 | B. | x2-5x+1=0 | C. | 2x2+5x+2=0 | D. | 2x2-5x+1=0 |
9.计算(-6)×(-1)的结果等于( )
| A. | 1 | B. | -1 | C. | 6 | D. | -6 |
16.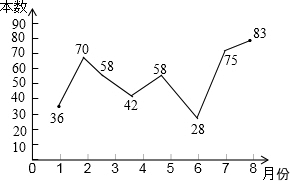 小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
 小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )| A. | 阅读数量的平均数是57 | B. | 阅读数量的众数是42 | ||
| C. | 阅读数量的中位数是58 | D. | 有4个月的阅读数量超过60本 |
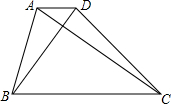 如图,梯形ABCD中,AD∥BC,AD=2,BC=8,AC=8,BD=6,则梯形ABCD的高为4.8.
如图,梯形ABCD中,AD∥BC,AD=2,BC=8,AC=8,BD=6,则梯形ABCD的高为4.8.