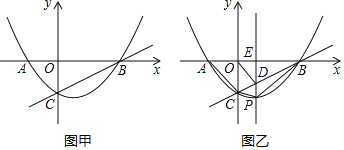
��Ŀ����
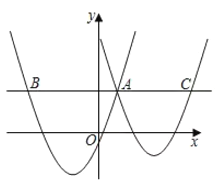
����Ŀ����ͼ��֪��������![]() �ύ�ڵ�C(0��4)����
�ύ�ڵ�C(0��4)����![]() �ύ��A(
�ύ��A(![]() ��0)��B(
��0)��B(![]() ��0)������
��0)������![]() ��
��![]() ����
����![]() ����������
����������
��1����������ߵĽ���ʽ��
��2����Q���߶�AB�ϵĶ��㣬����Q��QE��AC����BC�ڵ�E������CQ����Q(![]() ��0)����CQE�����Ϊ
��0)����CQE�����Ϊ![]() ����
����![]() ����
����![]() �ĺ�����ϵʽ����CQE����������ֵ��
�ĺ�����ϵʽ����CQE����������ֵ��
��3����M������Ϊ(2��0)���ʣ���ֱ��AC�ϣ��Ƿ���ڵ�F��ʹ�á�OMF�ǵ��������Σ������ڣ��������F�����꣬�������ڣ���˵�����ɣ�
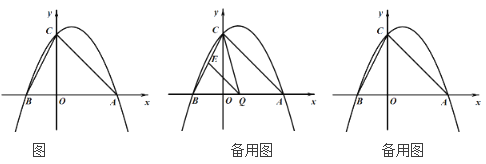
���𰸡���1��![]() ����2��
����2��![]() �� (����
�� (���У�![]() )����CQE����������ֵΪ3����3�����ڣ���F������Ϊ(1��3)��(2��2)��
)����CQE����������ֵΪ3����3�����ڣ���F������Ϊ(1��3)��(2��2)��
��������
��1���������÷������ͼ����x�ύ�����꣬������C������������a��ֵ���ɣ�
��2����EH��AB�ڵ�H���ɵ�EH��CO������QE��AC���ɵó�������ϵ���������EH�ij��ȣ����S��CQE���ó���ϵʽ���������ֵ��
��3�����ڣ����ô���ϵ�������AC�Ľ���ʽ����F��x��x��4������ʾ��OM��MF��OF�ij��ȣ�Ҫʹ��OMF�ǵ����������������������OF��FMʱ����OM��OF��2ʱ����OM��MFʱ���ֱ������F�����꣮
�⣺��1���ⷽ��![]() ��
��
�ã�![]() ��
��![]() ��
��
��A(4��0)��B(��2��0)��
�������߽���ʽΪ��![]() ��
��
��C(0��4)���룬��ã�![]() ��
��
�������߽���ʽΪ��
![]() ��
��![]() ��
��
��2����Q(![]() ��0)���ɵã�
��0)���ɵã�
BQ��![]() ��AQ��
��AQ��![]() ��
��
��EH��AB�ڵ�H��
��EH��CO����![]() ��
��
�֡�QE��AC����![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]()
![]() ��
��
��![]() ����
����![]() �ĺ�����ϵʽΪ��
�ĺ�����ϵʽΪ��
![]() ��
��
(����![]() )��
)��
���CQE����������ֵΪ3��
��3�����ڣ�
�������£�
��AC�Ľ���ʽΪ��![]() ��AC��A(4��0)��C(0��4)��
��AC��A(4��0)��C(0��4)��
��![]() ����֮�ã�
����֮�ã�![]() ��
��![]() ��
��
��AC�Ľ���ʽΪ��![]() ��
��
��![]() F��AC�ϣ���F(
F��AC�ϣ���F(![]() ��
��![]() )��
)��
��![]() ��
��
![]() ��
��![]() ��
��
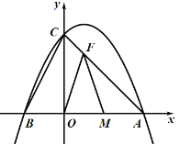
����OMF�ǵ��������ο��������������
��OF��FMʱ��F�ĺ�����ӦΪ1��
��F(1��3)��
��OF��OM��2ʱ��![]() ��
��
����ã�![]() ��
��
��![]() ����������������ڣ�
����������������ڣ�
�� OM��MF��2ʱ��![]() ��
��
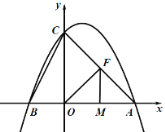
����ã�![]() ��
��
��ã�![]() ��
��![]() (��ȥ)��
(��ȥ)��
��F(2��2)��
��������������OMF�ǵ���������ʱ����F������Ϊ(1��3)��(2��2)��