题目内容
9.化简并求值:$\frac{1}{a}$+$\sqrt{\frac{1}{{a}^{2}}+{a}^{2}-2}$,其中a=$\frac{1}{5}$,一位同学的解答如下:$\frac{1}{a}$+$\sqrt{\frac{1}{{a}^{2}}+{a}^{2}-2}$
=$\frac{1}{a}$+$\sqrt{(a-\frac{1}{a})^{2}}$①
=$\frac{1}{a}$+a-$\frac{1}{a}$②
=a③
把a=$\frac{1}{5}$代入上式得:
原式=$\frac{1}{5}$④
(1)上述解题过程中,从哪一步开始出错?请填写处该步的代号:②.
(2)请写出错误的原因a-$\frac{1}{a}$<0.
(3)写出本题的正确解答过程.
分析 (1)根据二次根式的性质3可知第②开始出错;
(2)依据性质3知,a=$\frac{1}{5}$时a-$\frac{1}{a}$=$\frac{1}{5}-5$<0,故$\sqrt{(a-\frac{1}{a})^{2}}$=|a-$\frac{1}{a}$|;
(3)根据二次根式的性质先化简,再求值可得.
解答 解:(1)上述解题过程中,从第②开始出错,
故答案为:②;
(2)∵a=$\frac{1}{5}$时,a-$\frac{1}{a}$=$\frac{1}{5}-5$<0,
故答案为:a-$\frac{1}{a}$<0;
(3)原式=$\frac{1}{a}$+$\sqrt{(a-\frac{1}{a})^{2}}$
=$\frac{1}{a}$+|a-$\frac{1}{a}$|,
∵a=$\frac{1}{5}$时,a-$\frac{1}{a}$=$\frac{1}{5}-5$<0,
∴原式=$\frac{1}{a}$+$\frac{1}{a}$-a
=$\frac{2}{a}$-a,
当a=$\frac{1}{5}$时,
原式=10-$\frac{1}{5}$=$\frac{49}{5}$.
点评 本题主要考查二次根式的化简求值,熟练掌握二次根式的性质3是解题的关键.

练习册系列答案
相关题目
19.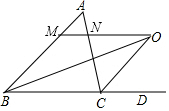 如图,△ABC中,BO平分∠ABC,CO平分△ABC的外角∠ACD,MN经过点O,与AB,AC相交于点M,N,且MN∥BC,则BM,CN之间的关系是( )
如图,△ABC中,BO平分∠ABC,CO平分△ABC的外角∠ACD,MN经过点O,与AB,AC相交于点M,N,且MN∥BC,则BM,CN之间的关系是( )
 如图,△ABC中,BO平分∠ABC,CO平分△ABC的外角∠ACD,MN经过点O,与AB,AC相交于点M,N,且MN∥BC,则BM,CN之间的关系是( )
如图,△ABC中,BO平分∠ABC,CO平分△ABC的外角∠ACD,MN经过点O,与AB,AC相交于点M,N,且MN∥BC,则BM,CN之间的关系是( )| A. | BM+CN=MN | B. | BM-CN=MN | C. | CN-BM=MN | D. | BM-CN=2MN |
4.小明做了以下4道计算题:①(-1)2010=2010;②0-(-1)=-l;③-$\frac{1}{2}$+$\frac{1}{3}$=-$\frac{1}{6}$;④$\frac{1}{2}$÷(-$\frac{1}{2}$)=-1.其中做对的共有( )
| A. | 1道 | B. | 2道 | C. | 3道 | D. | 4道 |
1.已知关于x的一元二次方程(k-1)x2+3x+k2-1=0有一根为0,则k=( )
| A. | ±1 | B. | 1 | C. | -1 | D. | 0 |
18.4,-3,0.04,-(-2),0,-|-5|,-2.1中的非负数有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
19.-$\frac{1}{5}$的相反数是( )
| A. | -5 | B. | $\frac{1}{5}$ | C. | -$\frac{1}{5}$ | D. | 5 |
 如图,是某时钟在平面镜中所成的像,请问该时刻实际应为9:30.
如图,是某时钟在平面镜中所成的像,请问该时刻实际应为9:30.