题目内容
19.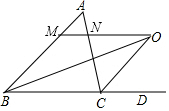 如图,△ABC中,BO平分∠ABC,CO平分△ABC的外角∠ACD,MN经过点O,与AB,AC相交于点M,N,且MN∥BC,则BM,CN之间的关系是( )
如图,△ABC中,BO平分∠ABC,CO平分△ABC的外角∠ACD,MN经过点O,与AB,AC相交于点M,N,且MN∥BC,则BM,CN之间的关系是( )| A. | BM+CN=MN | B. | BM-CN=MN | C. | CN-BM=MN | D. | BM-CN=2MN |
分析 只要证明BM=OM,ON=CN,即可解决问题.
解答 证明:∵ON∥BC,
∴∠MOC=∠OCD
∵CO平分∠ACD,
∴∠ACO=∠DCO,
∴∠NOC=∠OCN,
∴CN=ON,
∵ON∥BC,
∴∠MOB=∠OBD
∵BO平分∠ABC,
∴∠MBO=∠CBO,
∴∠MBO=∠MOB,
∴OM=BM
∵OM=ON+MN,OM=BM,ON=CN,
∴BM=CN+MN,
∴MN=BM-CN.
故选B.
点评 此题考查等腰三角形的判定和性质、平行线的性质等知识,解题的关键是证明等腰三角形,属于基础题.

练习册系列答案
相关题目
10.若分式$\frac{x-1}{2x+5}$有意义,则x的取值范围是( )
| A. | x≠1 | B. | x$≠-\frac{5}{2}$ | C. | x$>-\frac{5}{2}$ | D. | x$<-\frac{5}{2}$ |
14.下列计划图形,不一定是轴对称图形的是( )
| A. | 角 | B. | 等腰三角形 | C. | 长方形 | D. | 直角三角形 |
4.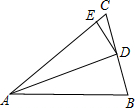 如图,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.则∠EDC的大小是( )
如图,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.则∠EDC的大小是( )
 如图,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.则∠EDC的大小是( )
如图,在△ABC中,AB=AC,BD=CD,∠BAD=20°,DE⊥AC于E.则∠EDC的大小是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
11.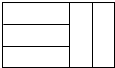 五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32cm,则小长方形的面积是( )
五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32cm,则小长方形的面积是( )
 五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32cm,则小长方形的面积是( )
五个完全相同的小长方形拼成如图所示的大长方形,大长方形的周长是32cm,则小长方形的面积是( )| A. | 8cm2 | B. | 10cm2 | C. | 12cm2 | D. | 16cm2 |
8.多项式4x2+□+1是一个完全平方式,那么“□”可以是( )
| A. | 2x | B. | -2x | C. | 4x | D. | -4x4 |
 如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F,且OF=1.
如图,AB为⊙O的直径,CD⊥AB于点E,交⊙O于点D,OF⊥AC于点F,且OF=1.