题目内容
5.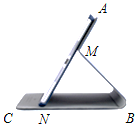 如图为一种平板电脑保护套的支架侧视图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架,为了观看舒适,可以调整倾斜角∠ANB的大小,但平板的下端点N只能在底座边CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图(见答题纸),其中AN表示平板电脑,M为AN上的定点,AN=CB=20 cm,AM=8 cm,MB=MN,根据以上数据,判断倾斜角∠ANB能小于30°吗?请说明理由.
如图为一种平板电脑保护套的支架侧视图,AM固定于平板电脑背面,与可活动的MB、CB部分组成支架,为了观看舒适,可以调整倾斜角∠ANB的大小,但平板的下端点N只能在底座边CB上.不考虑拐角处的弧度及平板电脑和保护套的厚度,绘制成图(见答题纸),其中AN表示平板电脑,M为AN上的定点,AN=CB=20 cm,AM=8 cm,MB=MN,根据以上数据,判断倾斜角∠ANB能小于30°吗?请说明理由.
分析 根据∠ANB=30°时,作ME⊥CB,垂足为E,根据锐角三角函数的定义求出EB及BN的长,进而可得出结论.
解答 解:当∠ANB=30°时,作ME⊥CB,垂足为E,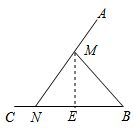
∵MB=MN,
∴∠B=∠ANB=30°.
在Rt△BEM中,
∵cosB=$\frac{EB}{MB}$,
∴EB=MB•cosB=(AN-AM)•cosB=6$\sqrt{3}$cm.
∵MB=MN,ME⊥BC,
∴BN=2BE=12$\sqrt{3}$cm.
∵CB=AN=20cm,且12$\sqrt{3}$>20,
∴此时N不在CB边上,与题目条件不符,随着∠ANB度数的减小,BN的长度增加,
∴倾斜角不可以小于30°.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
15.若关于x的方程$\frac{x}{x-2}$-$\frac{m}{{{x^2}-4}}$=1的解为正数,则m的取值范围是( )
| A. | m<4 | B. | m>4 | C. | m<4且m≠0 | D. | m>4且m≠8 |
17.抛物线y=ax2+bx+c与x轴交于点A、B,与y轴交于点C,O为坐标原点.若OB=OC=$\frac{1}{2}$OA,则b的值为 ( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | -1 |
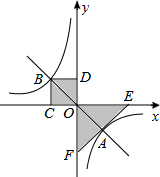 如图,过点O作直线与双曲线y=$\frac{k}{x}$(k≠0)交于A,B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴、y轴上分别取点E,F,使点A,E,F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1,S2的数量关系是2S1=S2.
如图,过点O作直线与双曲线y=$\frac{k}{x}$(k≠0)交于A,B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴、y轴上分别取点E,F,使点A,E,F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1,S2的数量关系是2S1=S2. 如图,已知点C为直线y=x上在第一象限内一点,直线y=2x+1交y轴于点A,交x轴于B,将直线AB沿射线OC方向平移$\sqrt{2}$个单位,则平移后直线的解析式为y=2x.
如图,已知点C为直线y=x上在第一象限内一点,直线y=2x+1交y轴于点A,交x轴于B,将直线AB沿射线OC方向平移$\sqrt{2}$个单位,则平移后直线的解析式为y=2x. 用五个完全相同的小正方体组成如图所示的立体图形,从上面看到的图形是( )
用五个完全相同的小正方体组成如图所示的立体图形,从上面看到的图形是( )


