题目内容
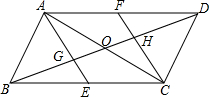 如图,在?ABCD中,对角线AC、BD相交于点O,作∠BAD和∠BCD的平分线,分别交BD于点G、H,延长AG交BC于点E,延长CH交AD于点F.
如图,在?ABCD中,对角线AC、BD相交于点O,作∠BAD和∠BCD的平分线,分别交BD于点G、H,延长AG交BC于点E,延长CH交AD于点F.(1)求证:△ABG≌△CDH;
(2)若∠BAE=2∠EAC,试判断四边形AECF是怎样的特殊四边形,并加以证明.
考点:平行四边形的性质,全等三角形的判定与性质
专题:
分析:(1)由在?ABCD中,可得AB∥CD,AB=CD,∠BAD=∠BCD,又由对角线AC、BD相交于点O,作∠BAD和∠BCD的平分线,分别交BD于点G、H,延长AG交BC于点E,延长CH交AD于点F,可得∠BAG=∠DCH,则可证得:△ABG≌△CDH;
(2)易证得△ABE≌△CDF(ASA),继而可得四边形AECF是平行四边形,然后由∠BAE=2∠EAC,可得∠EAC=∠CAF,继而证得AE=CE,则可得四边形AECF是菱形.
(2)易证得△ABE≌△CDF(ASA),继而可得四边形AECF是平行四边形,然后由∠BAE=2∠EAC,可得∠EAC=∠CAF,继而证得AE=CE,则可得四边形AECF是菱形.
解答:(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,∠BAD=∠BCD,
∴∠ABG=∠CDH,
∵AG,CH分别是∠BAD和∠BCD的平分线,
∴∠BAG=
∠BAD,∠DCH=
∠BCD,
∴∠BAG=∠DCH,
在△ABG和△CDH中,
,
∴△ABG≌△CDH(ASA);
(2)四边形AECF是菱形.
理由:∵AG平分∠BAD,
∴∠BAE=∠DAE,
∵∠BAE=2∠EAC,
∴∠DAE=2∠EAC,
∴∠EAC=∠FAC,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA),
∴BE=DF,
∵?ABCD中,AD∥BC,AD=BC,
∴AF=CE,
∴四边形AECF是平行四边形,
∴∠ACE=∠CAF,
∴∠ACE=∠CAE,
∴AE=EC,
∴四边形AECF是菱形.
∴AB∥CD,AB=CD,∠BAD=∠BCD,
∴∠ABG=∠CDH,
∵AG,CH分别是∠BAD和∠BCD的平分线,
∴∠BAG=
| 1 |
| 2 |
| 1 |
| 2 |

∴∠BAG=∠DCH,
在△ABG和△CDH中,
|
∴△ABG≌△CDH(ASA);
(2)四边形AECF是菱形.
理由:∵AG平分∠BAD,
∴∠BAE=∠DAE,
∵∠BAE=2∠EAC,
∴∠DAE=2∠EAC,
∴∠EAC=∠FAC,
在△ABE和△CDF中,
|
∴△ABE≌△CDF(ASA),
∴BE=DF,
∵?ABCD中,AD∥BC,AD=BC,
∴AF=CE,
∴四边形AECF是平行四边形,
∴∠ACE=∠CAF,
∴∠ACE=∠CAE,
∴AE=EC,
∴四边形AECF是菱形.
点评:此题考查了平行四边形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
下列函数中.y是x的反比例函数的是( )
A、y=
| ||||
B、y=-
| ||||
C、y=
| ||||
D、y=1-
|
以下说法中正确的是( )
| A、符号不同的数互为相反数 |
| B、除以一个数等于乘于这个数的倒数 |
| C、规定了原点、正方向和单位长度的直线叫做数轴 |
| D、一个数的绝对值越大,表示它的点在数轴上越靠右 |
当k•b<0时,一次函数y=kx-b的图象大致是( )
A、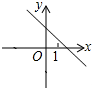 |
B、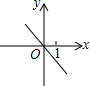 |
C、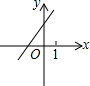 |
D、 |
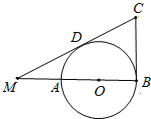 如图△MBC中,∠B=90°,∠C=60°,MB=2
如图△MBC中,∠B=90°,∠C=60°,MB=2