题目内容
2.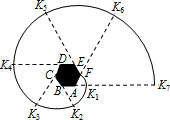 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中$\widehat{F{K}_{1}}$,$\widehat{{K}_{1}{K}_{2}}$,$\widehat{{K}_{2}{K}_{3}}$,$\widehat{{K}_{3}{K}_{4}}$,$\widehat{{K}_{4}{K}_{5}}$…的圆心依次按点A,B,C,D,E,F循环,分别记为l1,l2,l3,l4,l5,l6…当AB=1时,l2012等于$\frac{2012π}{3}$.
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中$\widehat{F{K}_{1}}$,$\widehat{{K}_{1}{K}_{2}}$,$\widehat{{K}_{2}{K}_{3}}$,$\widehat{{K}_{3}{K}_{4}}$,$\widehat{{K}_{4}{K}_{5}}$…的圆心依次按点A,B,C,D,E,F循环,分别记为l1,l2,l3,l4,l5,l6…当AB=1时,l2012等于$\frac{2012π}{3}$.
分析 如图,根据题意可以发现、判断,ln的半径为n,圆心角为60°,运用弧长公式即可解决问题.
解答  解:如图,∵六边形ABCDEF是正六边形,
解:如图,∵六边形ABCDEF是正六边形,
∴∠FAK1=180°-120°=60°;同理可求l2、l3…l2012的圆心角均为60°
∴${l}_{1}=\frac{60π•1}{180}=\frac{π}{3}$,${l}_{2}=\frac{60π•2}{180}=\frac{2π}{3}$,${l}_{3}=\frac{60π•3}{180}$=$\frac{3π}{3}$,
∴可以猜测:${l}_{n}=\frac{60π•n}{180}$,
∴${l}_{2012}=\frac{60π•2012}{180}$=$\frac{2012π}{3}$.
故答案为$\frac{2012π}{3}$.
点评 该题主要考查了弧长公式及其应用问题;为一道基础题;为考查弧长公式应用能力的一道好题.

练习册系列答案
相关题目
13.淮北市2013年1月7日至10日每天的最高气温与最低气温如下表:( )
其中温差最大的一天是( )
| 日期 | 1月7日 | 1月8日 | 1月9日 | 1月10日 |
| 最高气温 | 5℃ | 5℃ | 4℃ | 7℃ |
| 最低气温 | -5℃ | -3℃ | -4℃ | -5℃ |
| A. | 1月7日 | B. | 1月8日 | C. | 1月9日 | D. | 1月10日 |
17.直线y=2x-1一定经过点( )
| A. | (1,0) | B. | (1,2) | C. | (0,2) | D. | (0,-1) |
7.下列调查中应选择普查的是( )
| A. | 日光灯管厂要检测一批灯管的使用寿命 | |
| B. | 了解嘉兴市每天的流动人口数 | |
| C. | 了解浙江省城市居民日平均用水量 | |
| D. | 旅客上飞机前的安全检查 |
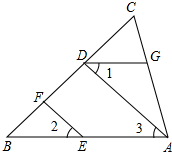 如图,已知EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
如图,已知EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整. 如图,由4个大小相同的正方体组合而成的几何体,其俯视图是( )
如图,由4个大小相同的正方体组合而成的几何体,其俯视图是( )


