题目内容
12.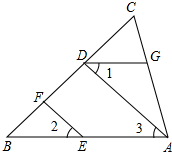 如图,已知EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
如图,已知EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.解:∵EF∥AD(已知)
∴∠2=∠3
又∵∠1=∠2(已知)
∴∠1=∠3(等量代换)
∴AB∥DG
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补)
∵∠BAC=70°(已知)
∴∠AGD=110°.
分析 根据平行线的性质和已知求出∠1=∠3,根据平行线的判定推出AB∥DG,根据平行线的性质推出∠BAC+∠DGA=180°即可.
解答 解:∵EF∥AD(已知),
∴∠2=∠3(两直线平行,同位角相等),
∵∠1=∠2,
∴∠1=∠3(等量代换),
∴AB∥DG(内错角相等,两直线平行),
∴∠BAC+∠DGA=180°(两直线平行,同旁内角互补),
∵∠BAC=70°,
∴∠AGD=110°,
故答案为:∠3,∠3,DG,∠AGD,(两直线平行,同旁内角互补),110°.
点评 本题考查了对平行线的性质和判定的应用,主要考查学生运用定理进行推理的能力,注意:①同位角相等,两直线平行,②内错角相等,两直线平行,③同旁内角互补,两直线平行,反之亦然.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.某商场连续7个月统计了A、B两种品牌的电视机的销售情况如下:(单位:台)
(1)分别求A、B两种品牌电视机月销售量的平均数、中位数和方差;
(2)你对这两种品牌电视机的销售情况做怎样的分析、推断.
| 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | |
| A | 10 | 14 | 17 | 16 | 13 | 14 | 14 |
| B | 6 | 10 | 14 | 15 | 16 | 17 | 20 |
(2)你对这两种品牌电视机的销售情况做怎样的分析、推断.
7. 如图是一个正方体的平面展开图,若把它折成一个正方体,则与空白面相对的面的字是( )
如图是一个正方体的平面展开图,若把它折成一个正方体,则与空白面相对的面的字是( )
 如图是一个正方体的平面展开图,若把它折成一个正方体,则与空白面相对的面的字是( )
如图是一个正方体的平面展开图,若把它折成一个正方体,则与空白面相对的面的字是( )| A. | 祝 | B. | 考 | C. | 试 | D. | 顺 |
17.以下四个标志图案是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
4.圆锥可以看做由下面哪个平面图形旋转得到?( )
| A. |  | B. |  | C. |  | D. |  |
1.探索规律:$\frac{1}{2},-\frac{3}{6},\frac{5}{12}$, ,$\frac{9}{30}$,空格内填( )
| A. | $\frac{7}{20}$ | B. | ${-}\frac{7}{20}$ | C. | $\frac{7}{18}$ | D. | $-\frac{7}{18}$ |
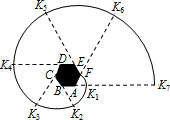 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中$\widehat{F{K}_{1}}$,$\widehat{{K}_{1}{K}_{2}}$,$\widehat{{K}_{2}{K}_{3}}$,$\widehat{{K}_{3}{K}_{4}}$,$\widehat{{K}_{4}{K}_{5}}$…的圆心依次按点A,B,C,D,E,F循环,分别记为l1,l2,l3,l4,l5,l6…当AB=1时,l2012等于$\frac{2012π}{3}$.
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中$\widehat{F{K}_{1}}$,$\widehat{{K}_{1}{K}_{2}}$,$\widehat{{K}_{2}{K}_{3}}$,$\widehat{{K}_{3}{K}_{4}}$,$\widehat{{K}_{4}{K}_{5}}$…的圆心依次按点A,B,C,D,E,F循环,分别记为l1,l2,l3,l4,l5,l6…当AB=1时,l2012等于$\frac{2012π}{3}$.