题目内容
3．
如图，在矩形ABCD中，对角线AC，BD交于点O，以下说法错误的是（ ）| A． | ∠ABC=90° | B． | AC=BD | C． | OA=OB | D． | OA=AB |
分析 利用排除法解决问题即可，只要证明A、B、C正确即可．
解答 解：∵四边形ABCD是矩形，
∴∠ABC=90°，AC=BD，OA=OC，OB=OD，
∴OA=OB，
故A、B、C正确，
故错误的是D，
故选D．
点评 本题考查矩形的性质，解题的关键是熟练掌握矩形的性质解决问题，属于基础题．
练习册系列答案
相关题目
14．下列命题中，原命题与逆命题均为真命题的有（ ）
①若|a|=|b|，则a2=b2；②若ma2＞na2，则m＞n；
③对顶角相等；④对角线互相平分的四边形是平行四边形．
①若|a|=|b|，则a2=b2；②若ma2＞na2，则m＞n；
③对顶角相等；④对角线互相平分的四边形是平行四边形．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
11．
五子棋的比赛规则是一人执黑子，一人执白子，两人轮流出棋，每次放一个棋子在棋盘的格点处，只要有同色的五个棋子先连成一条线（横、竖、斜均可）就获得胜利．如图是两人正在玩的一盘棋，若白棋A所在点的坐标是（-2，2），黑棋B所在点的坐标是（0，4），现在轮到黑棋走，黑棋放到点C的位置就获得胜利，点C的坐标是（ ）
五子棋的比赛规则是一人执黑子，一人执白子，两人轮流出棋，每次放一个棋子在棋盘的格点处，只要有同色的五个棋子先连成一条线（横、竖、斜均可）就获得胜利．如图是两人正在玩的一盘棋，若白棋A所在点的坐标是（-2，2），黑棋B所在点的坐标是（0，4），现在轮到黑棋走，黑棋放到点C的位置就获得胜利，点C的坐标是（ ）| A． | （3，3） | B． | （3，2） | C． | （5，2） | D． | （4，3） |
18．
矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），点D的坐标为（2，0），E为AB上的点，当△CDE的周长最小时，点E的坐标为（ ）
矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为（3，4），点D的坐标为（2，0），E为AB上的点，当△CDE的周长最小时，点E的坐标为（ ）| A． | （1，3） | B． | （3，1） | C． | （4，1） | D． | （3，2） |
8．$\frac{9}{16}$的平方根是（ ）
| A． | $\sqrt{\frac{3}{4}}$ | B． | ±$\sqrt{\frac{3}{4}}$ | C． | $\frac{3}{4}$ | D． | ±$\frac{3}{4}$ |
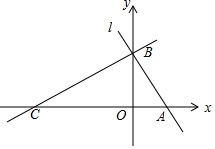如图，平面直角坐标系中，直线l：y=-$\sqrt{3}$x+$\sqrt{3}$分别交x轴，y轴于A，B两点，点C在x轴负半轴上，且∠ACB=30°．
在直角三角形ABC中，∠ACB=90°，∠A=50°，D是AB上的点，将△ACD沿直线CD翻折，使点A恰好落在BC上的点E处，则∠BDE=10°．
13．
如图，在△ABC中，∠C=90°，∠A=30°，BC=4cm，点D为AB的中点，则CD=（ ）
如图，在△ABC中，∠C=90°，∠A=30°，BC=4cm，点D为AB的中点，则CD=（ ）| A． | 3cm | B． | 4cm | C． | 5cm | D． | 6cm |