题目内容
12. 如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24 m,OE⊥CD于点E.已测得sin∠DOE=$\frac{12}{13}$.
如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24 m,OE⊥CD于点E.已测得sin∠DOE=$\frac{12}{13}$.(1)求AB的长;
(2)根据需要,水面要以每小时0.5m的速度下降,则经过多长时间才能将水排干?
分析 (1)根据三角函数可得到OD的值,进而得出AB的值;
(2)根据勾股定理求得OE的值,此时再求所需的时间就变得容易了.
解答 解:(1)∵OE⊥CD于点E,CD=24,
∴ED=$\frac{1}{2}$CD=12,
在Rt△DOE中,
∵sin∠DOE=$\frac{ED}{OD}=\frac{12}{13}$,
∴OD=13(m);
∴AB=26(m);
(2)OE=$\sqrt{O{D}^{2}-E{D}^{2}}=\sqrt{1{3}^{2}-1{2}^{2}}=5$,
∴将水排干需:5÷0.5=10(小时),
答:经过10小时才能将水排干.
点评 此题主要考查了学生对垂径定理及勾股定理的运用,关键是由垂径定理求DE,解直角三角形求半径OD,利用勾股定理求水面高度OE.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列说法正确的是( )
| A. | -1的倒数是1 | B. | -1的相反数是-1 | ||
| C. | 1的立方根是±1 | D. | 1的算术平方根是1 |
4.计算($\sqrt{12}$-$\sqrt{3}$)÷$\sqrt{3}$的结果是( )
| A. | -1 | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 1 |
 如图,将一块含45°的直角三角板的直角顶点放在直尺的一边上,∠1=75°,则∠2的度数是30°.
如图,将一块含45°的直角三角板的直角顶点放在直尺的一边上,∠1=75°,则∠2的度数是30°.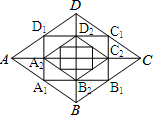 如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,…,如此下去,得到四边形A2016B2016C2016D2016的面积用含a,b的代数式表示为($\frac{1}{2}$)2017ab.
如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为顶点作菱形A2B2C2D2,…,如此下去,得到四边形A2016B2016C2016D2016的面积用含a,b的代数式表示为($\frac{1}{2}$)2017ab.