题目内容
1.已知△ABC的三边长分别为2$\sqrt{3}$,3$\sqrt{2}$,$\sqrt{30}$,与△ABC相似的△A′B′C′的最大边长为6$\sqrt{5}$.(1)求△A′B′C′的另外两边长;
(2)求△A′B′C′的面积及最大角的度数.
分析 (1)由题中条件可得三角形的相似比,根据相似三角形的性质进而可得其对应边的比,
(2)由勾股定理逆定理可得三角形为直角三角形,进而求得三角形的面积和最大角为90°.
解答 解:(1)∵△ABC∽△A′B′C′,
∴相似比为:$\frac{\sqrt{30}}{6\sqrt{5}}$=$\frac{\sqrt{6}}{6}$,
∴△A′B′C′的另外两边长是:6$\sqrt{2}$,6$\sqrt{3}$;
(2)∵(2$\sqrt{3}$)2+(3$\sqrt{2}$)2=30=($\sqrt{30}$)2,
∴△ABC与△A′B′C′是直角三角形,
∴△A′B′C′的面积=$\frac{1}{2}×$6$\sqrt{2}×6\sqrt{3}$=18$\sqrt{6}$,
最大角的度数=90°.
点评 本题主要考查了相似三角形的性质,以及勾股定理逆定理的运用,应熟练掌握.

练习册系列答案
相关题目
11.下列等式中是二元一次方程的是( )
| A. | x2+2x-3=0 | B. | x+2y=12 | C. | x+1=3x | D. | 5+8=13 |
9.下列说法正确的是( )
| A. | 三点确定一个圆 | |
| B. | 正多边形既是轴对称图形也是中心对称图形 | |
| C. | 等弧所对的圆周角相等 | |
| D. | 三角形的外心到三边的距离相等 |
10.下列说法中,一定正确的是( )
| A. | 有一个锐角相等的两个等腰三角形相似 | |
| B. | 底角为45°的两个等腰梯形相似 | |
| C. | 任意两个菱形相似 | |
| D. | 两个等腰直角三角形必相似 |
11.下列各式中,y是x的二次函数的是( )
| A. | y=x2-(x-2)2 | B. | x2+y-2=0 | C. | y=ax2+bx+c | D. | y=x2+3x-$\frac{1}{x}$ |
 如图,△ABD≌△ACE,点B和点C是对应顶点,AB=9cm,BD=7cm,AD=4cm,则DC=5cm.
如图,△ABD≌△ACE,点B和点C是对应顶点,AB=9cm,BD=7cm,AD=4cm,则DC=5cm.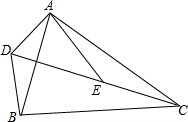 已知$\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$,求证:△ADB∽△AEC.
已知$\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$,求证:△ADB∽△AEC. 如图,$\frac{AB}{AD}$=$\frac{FB}{FE}$,AB=8cm,AD=2cm,BC=7.2cm,E是BC的中点,求EF,BF的长.
如图,$\frac{AB}{AD}$=$\frac{FB}{FE}$,AB=8cm,AD=2cm,BC=7.2cm,E是BC的中点,求EF,BF的长.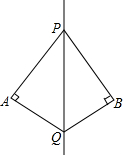 如图,PQ是∠APB的平分线,QA⊥PA于点A,QB⊥PB于点B,试判断点A,B是否关于PQ成轴对称,并说明理由.
如图,PQ是∠APB的平分线,QA⊥PA于点A,QB⊥PB于点B,试判断点A,B是否关于PQ成轴对称,并说明理由.