题目内容
18.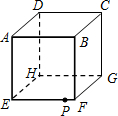 如图,是一个边长6分米的立方体ABCD---EFGH,一只甲虫在棱EF上且距离F点1分米的P处.它要爬到顶点D,需要爬行的最短距离是( )分米.
如图,是一个边长6分米的立方体ABCD---EFGH,一只甲虫在棱EF上且距离F点1分米的P处.它要爬到顶点D,需要爬行的最短距离是( )分米.| A. | 13 | B. | 12 | C. | 11 | D. | $\sqrt{157}$ |
分析 要求正方体中两点之间的最短路径,最直接的作法,就是将正方体展开,然后利用两点之间线段最短解答.
解答 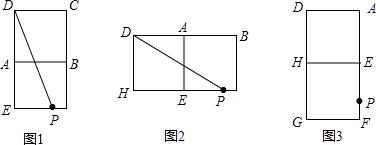 解:∵甲虫爬行的路径不能确定,
解:∵甲虫爬行的路径不能确定,
∴应分三种情况进行讨论:
(1)如图1所示:DP=$\sqrt{{DE}^{2}+{EP}^{2}}$=$\sqrt{{12}^{2}+{5}^{2}}$=13(cm);
(2)如图2所示:DP=$\sqrt{{DH}^{2}+{HP}^{2}}$=$\sqrt{{6}^{2}+{11}^{2}}$=$\sqrt{157}$(cm);
(3)如图3所示:DP=$\sqrt{{AD}^{2}+{AP}^{2}}$=$\sqrt{{6}^{2}+{11}^{2}}$=$\sqrt{157}$(cm).
∵13>$\sqrt{157}$,
∴甲虫爬行的最短距离是$\sqrt{157}$cm.
故选D.
点评 本题考查的是平面展开-最短路径问题,解答此类题目的关键是画出立方体的平面展开图,再利用勾股定理进行解答.

练习册系列答案
相关题目
13.计算(m+4)(m-4)的结果,正确的是( )
| A. | m2-4 | B. | m2+16 | C. | m2-16 | D. | m2+4 |
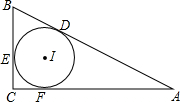 如图,⊙I是直角△ABC的内切圆,切点为D、E、F,若AF=10,BE=3,则△ABC的面积为30.
如图,⊙I是直角△ABC的内切圆,切点为D、E、F,若AF=10,BE=3,则△ABC的面积为30.