Question

2．一只兔子正在洞穴南面60m的地方觅食．一只狼在兔子正东80m处，此时兔子看到狼便急忙向自己的洞穴奔去，但狼以兔子速度的2倍跑向兔子洞穴处进行拦截．你认为兔子能死里逃生吗？请说明理由．

Answer 1

分析 根据勾股定理求得AB=100cm；求得兔子、狼的运动时间，通过比较它们到达目的地的时间可以判定兔子是否能够逃生．

解答 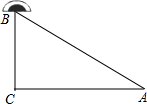解：如图，在直角△ABC中，∠C=90°，BC=60m，AC=80m，则由勾股定理得到：AB=$\sqrt{B{C}^{2}+A{C}^{2}}$=$\sqrt{6{0}^{2}+8{0}^{2}}$=100（m）．
设兔子的运动速度是xm/h，
则兔子由点C到达点B需要的时间是$\frac{60}{x}$；
狼由点A到点B需要的时间是$\frac{100}{2x}$=$\frac{50}{x}$，
∵$\frac{60}{x}$＞$\frac{50}{x}$，
∴兔子不能死里逃生．

点评 本题考查了勾股定理的应用．在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．