题目内容
已知n个不同的数x1,x2,x3,…,xn是正整数1,2,…,n的任意一个排列,试求|x1-1|+|x2-2|+…+|xn-n|的最小值.
考点:绝对值
专题:
分析:分别求出当n为偶数时,当n为奇数时,求出各式的最值,进而得出答案.
解答:解:当n为偶数时,
当x=
时,|x1-1|+|x2-2|+…+|xn-n|的值最小为:
-1+
-2+…+0+1+…+
=
,
当n为奇数时,x=
时,|x1-1|+|x2-2|+…+|xn-n|的值最小为:
-
+
-
+…+0+1+…+
-
=
.
当x=
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
| n |
| 2 |
=
| n2 |
| 4 |
当n为奇数时,x=
| n+1 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
| n |
| 2 |
| 3 |
| 2 |
| n |
| 2 |
| 1 |
| 2 |
=
| n2-1 |
| 4 |
点评:此题主要考查了绝对值,利用分类讨论得出是解题关键.

练习册系列答案
相关题目
若关于x的一元二次方程(m-2)x2+3x+m2-4=0的常数项为0,则m的值等于( )
| A、-2 | B、2 | C、-2或2 | D、0 |
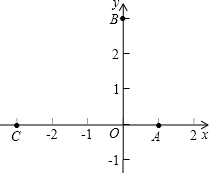 如图,已知点A(1,0),B(0,3),C(-3,0),动点P(x,y)在线段AB上,CP交y轴于点D,设BD的长为t.
如图,已知点A(1,0),B(0,3),C(-3,0),动点P(x,y)在线段AB上,CP交y轴于点D,设BD的长为t. 小明从黄山百步云梯脚下的点A约走了50m后,到达山顶的点B.已知山顶B到山脚下的垂直距离约是30m,求山坡的坡度.
小明从黄山百步云梯脚下的点A约走了50m后,到达山顶的点B.已知山顶B到山脚下的垂直距离约是30m,求山坡的坡度.