题目内容
已知二次函数y=x2-2mx+m2-1.
(1)该抛物线与y轴交于点C(0,
),顶点为D,求点D的坐标.
(2)在(1)的条件下,x轴是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.?
(1)该抛物线与y轴交于点C(0,
| 3 |
| 4 |
(2)在(1)的条件下,x轴是否存在一点P,使得PC+PD最短?若P点存在,求出P点的坐标;若P点不存在,请说明理由.?
考点:二次函数的性质,轴对称-最短路线问题
专题:计算题
分析:(1)把C点坐标代入解析式可计算出m=±
,然后把解析式配成顶点式即可得到D点坐标;
(2)分类讨论:先利用待定系数法求出直线CD的解析式,然后求出直线CD与x轴的交点坐标,即可得到P点坐标.
| ||
| 2 |
(2)分类讨论:先利用待定系数法求出直线CD的解析式,然后求出直线CD与x轴的交点坐标,即可得到P点坐标.
解答:解:(1)把C(0,
)代入y=x2-2mx+m2-1得m2-1=
,解得m=±
,
所以y=(x-m)2-1=(x±
)2-1,
所以D点坐标为(
,-1)或(-
,-1)
(2)存在.
当D点坐标为(
,-1),设直线CD的解析式为y=kx+b,把C(0,
)、D(
,-1)代入得
,解得
,
则直线CD的解析式为y=-
x+
,当y=0时,-
x+
=0,解得x=
,此时P点坐标为(
,0);
当D点坐标为(-
,-1),设直线CD的解析式为y=kx+b,把C(0,
)、D(-
,-1)代入得
,解得
,
则直线CD的解析式为y=
x+
,当y=0时,
x+
=0,解得x=-
,此时P点坐标为(-
,0),
所以满足条件的P点坐标为(
,0)或(-
,0).
| 3 |
| 4 |
| 3 |
| 4 |
| ||
| 2 |
所以y=(x-m)2-1=(x±
| ||
| 2 |
所以D点坐标为(
| ||
| 2 |
| ||
| 2 |
(2)存在.
当D点坐标为(
| ||
| 2 |
| 3 |
| 4 |
| ||
| 2 |
|
|
则直线CD的解析式为y=-
| ||
| 2 |
| 3 |
| 4 |
| ||
| 2 |
| 3 |
| 4 |
3
| ||
| 14 |
3
| ||
| 14 |
当D点坐标为(-
| ||
| 2 |
| 3 |
| 4 |
| ||
| 2 |
|
|
则直线CD的解析式为y=
| ||
| 2 |
| 3 |
| 4 |
| ||
| 2 |
| 3 |
| 4 |
3
| ||
| 14 |
3
| ||
| 14 |
所以满足条件的P点坐标为(
3
| ||
| 14 |
3
| ||
| 14 |
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.
②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目




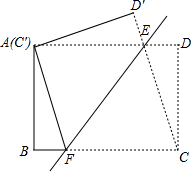 如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.求证:四边形AFCE为菱形.
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E、交BC于点F,连接AF、CE.求证:四边形AFCE为菱形.