题目内容
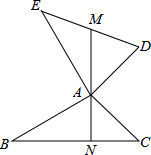 已知AE⊥AB,DA⊥AC,AE=AB,AD=AC.直线MN过点A,交DE、BC于点M、N.
已知AE⊥AB,DA⊥AC,AE=AB,AD=AC.直线MN过点A,交DE、BC于点M、N.(1)若AM是△EAD中线,求证:AN⊥BC;
(2)若AN⊥BC,求证:EM=DM.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)延长AM至F,使MF=AM,然后利用“边角边”证明△EMF和△DMA全等,根据全等三角形对应角相等可得∠DAM=∠F,全等三角形对应边相等可得EF=AD,然后根据同角的补角相等求出∠BAC=∠AEF,再利用“边角边”证明△ABC和△EAF全等,根据全等三角形对应角相等可得∠EAF=∠B,再求出∠ANB=90°,从而得证;
(2)过点E作EF∥AD交AM的延长线于F,根据两直线平行,内错角相等可得∠F=∠DAM,根据同角的余角相等求出∠EAF=∠B,然后求出∠BAC=∠AEF,再利用“角角边”证明△ABC和△EAF全等,根据全等三角形对应边可得EF=AC,然后求出EF=AD,再利用“角角边”证明△EFM和△DAM全等,根据全等三角形对应边相等可得EM=DM.
(2)过点E作EF∥AD交AM的延长线于F,根据两直线平行,内错角相等可得∠F=∠DAM,根据同角的余角相等求出∠EAF=∠B,然后求出∠BAC=∠AEF,再利用“角角边”证明△ABC和△EAF全等,根据全等三角形对应边可得EF=AC,然后求出EF=AD,再利用“角角边”证明△EFM和△DAM全等,根据全等三角形对应边相等可得EM=DM.
解答:证明:(1)如图,延长AM至F,使MF=AM,
∵AM是△EAD中线,
∴EM=DM,
在△EMF和△DMA中,
,
∴△EMF≌△DMA(SAS),
∴∠DAM=∠F,EF=AD,
∵AD=AC,
∴EF=AC,
∵AE⊥AB,DA⊥AC,
∴∠BAC=360°-90°×2-∠DAE=180°-∠DAE,
∵∠AEF=180°-∠F-∠EAM=180°-∠DAM-∠EAM=180°-∠DAE,
∴∠BAC=∠AEF,
在△ABC和△EAF中,
,
∴△ABC≌△EAF(SAS),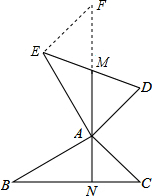
∴∠EAF=∠B,
∵AE⊥AB,
∴∠EAF+∠BAN=90°,
∴∠B+∠BAN=90°,
在△ABN中,∠ANB=180°-(∠B+∠BAN)=180°-90°=90°,
∴AN⊥BC;
(2)如图,过点E作EF∥AD交AM的延长线于F,
则∠F=∠DAM,
∵DA⊥AC,
∴∠DAM+∠CAN=90°,
∵AN⊥BC,
∴∠CAN+∠C=90°,
∴∠F=∠DAM=∠C,
∵AE⊥AB,DA⊥AC,
∴∠BAC=360°-90°×2-∠DAE=180°-∠DAE,
∵∠AEF=180°-∠F-∠EAM=180°-∠DAM-∠EAM=180°-∠DAE,
∴∠BAC=∠AEF,
在△ABC和△EAF中,
,
∴△ABC≌△EAF(AAS),
∴EF=AC,
∵AD=AC,
∴EF=AD,
在△EFM和△DAM中,
,
∴△EFM≌△DAM(AAS),
∴EM=DM.
∵AM是△EAD中线,
∴EM=DM,
在△EMF和△DMA中,
|
∴△EMF≌△DMA(SAS),
∴∠DAM=∠F,EF=AD,
∵AD=AC,
∴EF=AC,
∵AE⊥AB,DA⊥AC,
∴∠BAC=360°-90°×2-∠DAE=180°-∠DAE,
∵∠AEF=180°-∠F-∠EAM=180°-∠DAM-∠EAM=180°-∠DAE,
∴∠BAC=∠AEF,
在△ABC和△EAF中,
|
∴△ABC≌△EAF(SAS),

∴∠EAF=∠B,
∵AE⊥AB,
∴∠EAF+∠BAN=90°,
∴∠B+∠BAN=90°,
在△ABN中,∠ANB=180°-(∠B+∠BAN)=180°-90°=90°,
∴AN⊥BC;
(2)如图,过点E作EF∥AD交AM的延长线于F,
则∠F=∠DAM,
∵DA⊥AC,
∴∠DAM+∠CAN=90°,
∵AN⊥BC,
∴∠CAN+∠C=90°,
∴∠F=∠DAM=∠C,
∵AE⊥AB,DA⊥AC,
∴∠BAC=360°-90°×2-∠DAE=180°-∠DAE,
∵∠AEF=180°-∠F-∠EAM=180°-∠DAM-∠EAM=180°-∠DAE,
∴∠BAC=∠AEF,
在△ABC和△EAF中,
|
∴△ABC≌△EAF(AAS),
∴EF=AC,
∵AD=AC,
∴EF=AD,
在△EFM和△DAM中,
|
∴△EFM≌△DAM(AAS),
∴EM=DM.
点评:本题考查了全等三角形的判定与性质,同角的余角相等,同角的补角相等的性质,难点在于作辅助线构造出全等三角形并二次证明三角形全等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图是窗子的形状,它是由上下连成一体的两个矩形构成,已知窗框的用料是6m,要使窗子能透过最多的光线,问窗子的各边长是多少?
如图是窗子的形状,它是由上下连成一体的两个矩形构成,已知窗框的用料是6m,要使窗子能透过最多的光线,问窗子的各边长是多少?