题目内容
 如图是窗子的形状,它是由上下连成一体的两个矩形构成,已知窗框的用料是6m,要使窗子能透过最多的光线,问窗子的各边长是多少?
如图是窗子的形状,它是由上下连成一体的两个矩形构成,已知窗框的用料是6m,要使窗子能透过最多的光线,问窗子的各边长是多少?考点:二次函数的应用
专题:
分析:光线最多就是面积最大,可设宽为xm,则长为(6-3x)÷2=3-
xm,表示出面积,运用函数性质求解.
| 3 |
| 2 |
解答:解:设窗户的宽为xm,则长为(6-3x)÷2=3-
xm,
窗户的面积S=x(3-
x)=-
x2+3x=-
(x-1)2+
,
当x=1时,S有最大值为
,
即窗户的长为
m,宽为1m.
| 3 |
| 2 |
窗户的面积S=x(3-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
当x=1时,S有最大值为
| 3 |
| 2 |
即窗户的长为
| 3 |
| 2 |
点评:本题主要考查了二次函数的应用,解答本题的关键是理解光线最多就是窗子面积最大时,据此求面积表达式,运用函数性质求解.

练习册系列答案
相关题目
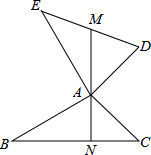 已知AE⊥AB,DA⊥AC,AE=AB,AD=AC.直线MN过点A,交DE、BC于点M、N.
已知AE⊥AB,DA⊥AC,AE=AB,AD=AC.直线MN过点A,交DE、BC于点M、N. O为矩形ABCD对角线的交点,DF平分∠ADC交AC于点E,交BC于点F,若∠BDF=15°,求∠BFO.
O为矩形ABCD对角线的交点,DF平分∠ADC交AC于点E,交BC于点F,若∠BDF=15°,求∠BFO.