题目内容
试确定一切有理数r,使关于x的二次方程rx2+(r+2)x+3r-2=0有根且只有整数根,求r的值.
考点:一元二次方程的整数根与有理根
专题:
分析:由于方程的类型已经确定,则r≠0,由根与系数关系得到关于r的两个等式,利用因式(数)分解先求出方程两整数根.
解答:解:由题意可得:
r≠0时,因为方程有整数根,所以两根之和为整数,两根之积也为整数,
而x1+x2=
=-1-
,
x1x2=
=3-
,
所以-1-
,3-
都应该是整数,
所以r是2的因数,而2的因数有±1,±2,
所以r=±1或r=±2,当r=1或2时,方程没有实数根,所以不合题意,舍去;
而当r=-1时,方程变为-x2+x-5=0,方程有实数根,但不是整数,不符合题意,舍去;
当r=-2时,方程变为-2x2-8=0,
解得:x=±2,符合题意;
综合以上得r=-2.
r≠0时,因为方程有整数根,所以两根之和为整数,两根之积也为整数,
而x1+x2=
| -(r+2) |
| r |
| 2 |
| r |
x1x2=
| 3r-2 |
| r |
| 2 |
| r |
所以-1-
| 2 |
| r |
| 2 |
| r |
所以r是2的因数,而2的因数有±1,±2,
所以r=±1或r=±2,当r=1或2时,方程没有实数根,所以不合题意,舍去;
而当r=-1时,方程变为-x2+x-5=0,方程有实数根,但不是整数,不符合题意,舍去;
当r=-2时,方程变为-2x2-8=0,
解得:x=±2,符合题意;
综合以上得r=-2.
点评:本题主要考查了一元二次方程的整数根与有理根.在解答此题时,利用了一元二次方程的根与系数的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
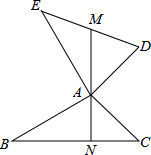 已知AE⊥AB,DA⊥AC,AE=AB,AD=AC.直线MN过点A,交DE、BC于点M、N.
已知AE⊥AB,DA⊥AC,AE=AB,AD=AC.直线MN过点A,交DE、BC于点M、N. O为矩形ABCD对角线的交点,DF平分∠ADC交AC于点E,交BC于点F,若∠BDF=15°,求∠BFO.
O为矩形ABCD对角线的交点,DF平分∠ADC交AC于点E,交BC于点F,若∠BDF=15°,求∠BFO.