题目内容
 如图,要在一面靠墙(墙长18米)的地方用30米长的不锈钢修建一个面积为100平方米的矩形花圃的护栏,问:围成的花圃的长和宽分别是多少?
如图,要在一面靠墙(墙长18米)的地方用30米长的不锈钢修建一个面积为100平方米的矩形花圃的护栏,问:围成的花圃的长和宽分别是多少?考点:一元二次方程的应用
专题:几何图形问题
分析:设矩形场地的长为xm,那么宽为(30-x)÷2m,然后根据矩形面积公式列方程求解即可解决问题.
解答:解:设矩形场地的长为xm,
由题意列方程得x×
=100,
整理得x2-30x+200=0,
解得:x1=20,x2=10.
又∵墙面长为18m,
∴x=20不符合题意,应舍去.
∴x=10.
答:围成的花圃的长和宽分别是10m,10m.
由题意列方程得x×
| 30-x |
| 2 |
整理得x2-30x+200=0,
解得:x1=20,x2=10.
又∵墙面长为18m,
∴x=20不符合题意,应舍去.
∴x=10.
答:围成的花圃的长和宽分别是10m,10m.
点评:本题考查的是一元二次方程的应用,要会把实际问题的数量关系转化成一元二次方程的问题解决,难度一般.

练习册系列答案
相关题目
计算(-3m)2的结果是( )
| A、6m2 |
| B、3m2 |
| C、-9m2 |
| D、9m2 |
Rt△ABC两直角边的长分别为6cm和8cm,则连接这两条直角边中点的线段长为( )
| A、10cm | B、3cm |
| C、4cm | D、5cm |
若c为实数,方程x2-3x+c=0的一个根的相反数是方程x2+3x-c=0的一个根,那么方程x2-3x+c=0的根是
( )
( )
| A、1,2 | B、0,3 |
| C、-1,-2 | D、0,-3 |
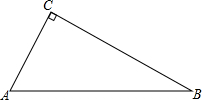 如图所示,在直角三角形ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点B旋转90°,得到关于点A的对称点D,则AD的长是( )
如图所示,在直角三角形ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点B旋转90°,得到关于点A的对称点D,则AD的长是( )| A、20 | ||
| B、10 | ||
C、10
| ||
D、20
|
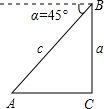 如图所示,飞行员在飞机B上用雷达测得飞机与目标城市A的距离c为4.5×102m,且测得对这个目标的俯角α=45°,设地面是平的,求飞机此时的高度a.
如图所示,飞行员在飞机B上用雷达测得飞机与目标城市A的距离c为4.5×102m,且测得对这个目标的俯角α=45°,设地面是平的,求飞机此时的高度a.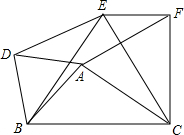 如图,以△ABC的三边为边在BC同一侧分别作三个等边三角形△ABD、△BCE、△ACF.
如图,以△ABC的三边为边在BC同一侧分别作三个等边三角形△ABD、△BCE、△ACF.