题目内容
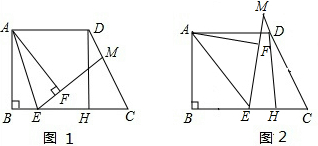
如图1,在四边形ABCD中,AD∥BC,AB⊥BC,AD=CD,∠C=60°,DH⊥BC于点H,点E是BC上一点,连接AE,将△ABE沿AE翻折,点B落在点F处,射线EF交CD所在直线于点M
(1)若点M在CD边上时,求证:FM-DM=CH;
(2)如图2,若点M在CD边得延长线上时,FM、DM、CH三条线段有怎样得数量关系?说明理由.
(1)若点M在CD边上时,求证:FM-DM=CH;
(2)如图2,若点M在CD边得延长线上时,FM、DM、CH三条线段有怎样得数量关系?说明理由.

考点:全等三角形的判定与性质,翻折变换(折叠问题)
专题:
分析:(1)利用过点A作AG⊥CD,交CD的延长线于点G,连接AM,进而利用HL定理得出Rt△AMG≌Rt△AMF,求出MG=MF,即可得出答案;
(2)过点A作AG⊥CD,交CD的延长线于点G,连接AM,AC,进而利用HL定理得出Rt△AMG≌Rt△AMF,求出MG=MF,即可得出答案.
(2)过点A作AG⊥CD,交CD的延长线于点G,连接AM,AC,进而利用HL定理得出Rt△AMG≌Rt△AMF,求出MG=MF,即可得出答案.
解答:(1)证明:过点A作AG⊥CD,交CD的延长线于点G,连接AM,
∵AD∥BC,
∴∠ACB=∠DAC,
∵AD=CD,
∴∠ACD=∠DAC
∴∠ACB=∠ACD,
∴AG=AB
∵AB=AF,
∴AG=AF
又∵AM=AM,
在Rt△AMG和Rt△AMF中,
∴Rt△AMG≌Rt△AMF(HL),
∴FM=GM,
∴FM一DM=GD,
在Rt△AGD和Rt△DHC中,AD=DC,AG=DH,由勾股定理得:DG=CH,
∴FM-DM=CH;

(2)FM+DM=CH,
理由是:过点A作AG⊥CD,交CD的延长线于点G,连接AM,AC,
∵AD∥BC,
∴∠ACB=∠DAC,
∵AD=CD,
∴∠ACD=∠DAC
∴∠ACB=∠ACD,
∴AG=AB
∵AB=AF,
∴AG=AF,
又∵AM=AM,
在Rt△AMG和Rt△AMF中,
∴Rt△AMG≌Rt△AMF(HL),
∴FM=GM,
∴FM+DM=GD,
在Rt△AGD和Rt△DHC中,AD=DC,AG=DH,由勾股定理得:DG=CH,
∴FM+DM=CH.
∵AD∥BC,
∴∠ACB=∠DAC,
∵AD=CD,
∴∠ACD=∠DAC
∴∠ACB=∠ACD,
∴AG=AB
∵AB=AF,
∴AG=AF
又∵AM=AM,
在Rt△AMG和Rt△AMF中,
|
∴Rt△AMG≌Rt△AMF(HL),
∴FM=GM,
∴FM一DM=GD,
在Rt△AGD和Rt△DHC中,AD=DC,AG=DH,由勾股定理得:DG=CH,
∴FM-DM=CH;

(2)FM+DM=CH,
理由是:过点A作AG⊥CD,交CD的延长线于点G,连接AM,AC,
∵AD∥BC,
∴∠ACB=∠DAC,
∵AD=CD,
∴∠ACD=∠DAC
∴∠ACB=∠ACD,
∴AG=AB
∵AB=AF,
∴AG=AF,
又∵AM=AM,
在Rt△AMG和Rt△AMF中,
|
∴Rt△AMG≌Rt△AMF(HL),
∴FM=GM,
∴FM+DM=GD,
在Rt△AGD和Rt△DHC中,AD=DC,AG=DH,由勾股定理得:DG=CH,
∴FM+DM=CH.
点评:此题主要考查了翻折变换的性质以及全等三角形的判定等知识,根据已知得出全等三角形进而得出对应角对应边的关系是解题关键.

练习册系列答案
相关题目
若c为实数,方程x2-3x+c=0的一个根的相反数是方程x2+3x-c=0的一个根,那么方程x2-3x+c=0的根是
( )
( )
| A、1,2 | B、0,3 |
| C、-1,-2 | D、0,-3 |
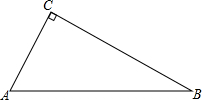 如图所示,在直角三角形ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点B旋转90°,得到关于点A的对称点D,则AD的长是( )
如图所示,在直角三角形ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点B旋转90°,得到关于点A的对称点D,则AD的长是( )| A、20 | ||
| B、10 | ||
C、10
| ||
D、20
|
 如图①,图②,图③…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第20个“广”字中的棋子个数是( )
如图①,图②,图③…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第20个“广”字中的棋子个数是( )| A、43 | B、44 | C、45 | D、46 |
 如图几何体的左视图是( )
如图几何体的左视图是( )A、 |
B、 |
C、 |
D、 |
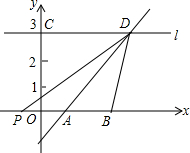 如图,在直角坐标平面内,直线y=x-1与x轴交于点A,过点C(0,3)的直线l∥x轴,与直线y=x-1交于点D,点P从原点O出发沿x轴负半轴移动,连接PD,设点P移动的距离为m.
如图,在直角坐标平面内,直线y=x-1与x轴交于点A,过点C(0,3)的直线l∥x轴,与直线y=x-1交于点D,点P从原点O出发沿x轴负半轴移动,连接PD,设点P移动的距离为m. 如图,正方形ABCD的边长为4,点M,N,P分别为AD,BC,CD的中点.现从点P观察线段AB,当长度为1的线段l(图中的黑粗线)以每秒1个单位长的速度沿线段MN从左向右运动时,l将阻挡部分观察视线,在△PAB区域内形成盲区.设l的左端点从M点开始,运动时间为t秒(0≤t≤3).设△PAB区域内的盲区面积为y(平方单位).
如图,正方形ABCD的边长为4,点M,N,P分别为AD,BC,CD的中点.现从点P观察线段AB,当长度为1的线段l(图中的黑粗线)以每秒1个单位长的速度沿线段MN从左向右运动时,l将阻挡部分观察视线,在△PAB区域内形成盲区.设l的左端点从M点开始,运动时间为t秒(0≤t≤3).设△PAB区域内的盲区面积为y(平方单位).