题目内容
20. 如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上.若△ABC的边BC长为40厘米,高AH为30厘米,则正方形DEFG的边长为$\frac{120}{7}$厘米.
如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上.若△ABC的边BC长为40厘米,高AH为30厘米,则正方形DEFG的边长为$\frac{120}{7}$厘米.
分析 由DG∥BC得△ADG∽△ABC,利用相似三角形对应边上高的比等于相似比,列方程求解.
解答 解:设正方形的边长为x.
由正方形DEFG得,DG∥EF,即DG∥BC,
∵AH⊥BC,
∴AP⊥DG.
由DG∥BC得△ADG∽△ABC
∴$\frac{DG}{BC}$=$\frac{AP}{AH}$.
∵PH⊥BC,DE⊥BC
∴PH=ED,AP=AH-PH,
即$\frac{DG}{BC}=\frac{AH-PH}{AH}$,
由BC=40,AH=30,DE=DG=x,
得$\frac{x}{40}=\frac{30-x}{30}$,
解得x=$\frac{120}{7}$.
故正方形DEFG的边长是$\frac{120}{7}$.
故答案为:$\frac{120}{7}$.
点评 本题考查了相似三角形的判定与性质.关键是由平行线得到相似三角形,利用相似三角形的性质列方程.

练习册系列答案
相关题目
8.下列有理数大小关系判断正确的是( )
| A. | 0>|-10| | B. | -(-$\frac{1}{9}$)>-|-$\frac{1}{10}$| | C. | |-3|<|+3| | D. | -1>-0.01 |
15. 把原来弯曲的河道改直,两地间的河道长度会变短,这其中蕴含的数学道理是( )
把原来弯曲的河道改直,两地间的河道长度会变短,这其中蕴含的数学道理是( )
 把原来弯曲的河道改直,两地间的河道长度会变短,这其中蕴含的数学道理是( )
把原来弯曲的河道改直,两地间的河道长度会变短,这其中蕴含的数学道理是( )| A. | 两地之间线段最短 | B. | 直线比曲线短 | ||
| C. | 两点之间直线最短 | D. | 两点确定一条直线 |
10.一种病毒的长度约为0.000072mm,用科学记数法表示0.000072的结果为( )
| A. | 7.2×10-5 | B. | -7.2×105 | C. | 7.2×106 | D. | -7.2×10-6 |
 如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=35°,则∠BAD=55°.
如图,在⊙O中,AB为直径,CD为弦,已知∠ACD=35°,则∠BAD=55°. 如图,已知△ABC≌△ABD,∠CAB=30°,∠D=40°,则∠CBE=70°.
如图,已知△ABC≌△ABD,∠CAB=30°,∠D=40°,则∠CBE=70°.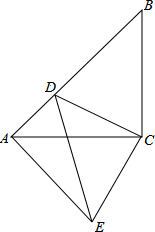 如图所示,在△ACB中,∠ACB=90°,CA=CB,D为AB边上一点,连结CD,CD绕点C逆时针旋转90度与线段CE重合,连结AE.
如图所示,在△ACB中,∠ACB=90°,CA=CB,D为AB边上一点,连结CD,CD绕点C逆时针旋转90度与线段CE重合,连结AE.