题目内容
某厂从2010年开始投入技改资金,经技术改进后,其产品的生产成本不断降低,具体数据如下表:
请你认真分析表中数据,从你所学习过的一次函数和反比例函数中确定一种函数来表示其变化规律,说明确定是这种函数而不是另一种函数的理由,并求出它的函数表达式.
| 年度 | 2010 | 2011 | 2012 | 2013 |
| 投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
考点:反比例函数的应用
专题:
分析:根据实际题意和数据特点分情况求解,根据排除法可知其为反比例函数,利用待定系数法求解即可;
解答:解:设其为一次函数,解析式为y=kx+b,
∵当x=2.5时,y=7.2;当x=3时,y=6,
∴
,
解得k=-2.4,b=13.2,
∴一次函数解析式为y=-2.4x+13.2,
把x=4时,y=4.5代入此函数解析式,
左边≠右边.
∴其不是一次函数.
同理.其也不是二次函数.
设其为反比例函数.解析式为y=
.
∵当x=2.5时,y=7.2,
∴7.2=
,
解得k=18
∴反比例函数是y=
.
验证:当x=3时,y=
=6,符合反比例函数.
同理可验证x=4时,y=4.5,x=4.5时,y=4成立.
可用反比例函数y=
表示其变化规律.
∵当x=2.5时,y=7.2;当x=3时,y=6,
∴
|
解得k=-2.4,b=13.2,
∴一次函数解析式为y=-2.4x+13.2,
把x=4时,y=4.5代入此函数解析式,
左边≠右边.
∴其不是一次函数.
同理.其也不是二次函数.
设其为反比例函数.解析式为y=
| k |
| x |
∵当x=2.5时,y=7.2,
∴7.2=
| k |
| 2.5 |
解得k=18
∴反比例函数是y=
| 18 |
| x |
验证:当x=3时,y=
| 18 |
| 3 |
同理可验证x=4时,y=4.5,x=4.5时,y=4成立.
可用反比例函数y=
| 18 |
| x |
点评:主要考查了反比例函数的应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式,再根据自变量的值求算对应的函数值.要注意用排除法确定函数的类型.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
将一个图形先顺时针旋转30°,再平移2cm,得到另一个图形,则这两个图形( )
| A、形状改变 | B、大小改变 |
| C、位置不变 | D、大小不变 |

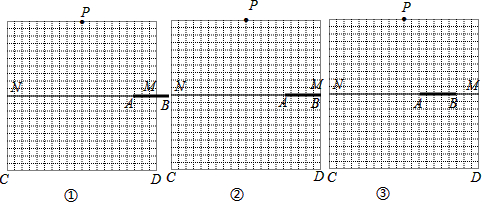
 如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,请根据图中所标数据求∠ACB的大小,并且求当轮船距离灯塔C最近时,∠ACB是多少度?
如图,一艘轮船按箭头所示方向行驶,C处有一灯塔,请根据图中所标数据求∠ACB的大小,并且求当轮船距离灯塔C最近时,∠ACB是多少度?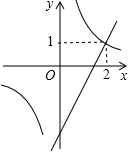 如图,已知反比例函数
如图,已知反比例函数 如图,在?ABCD中,点E,F分别在AD,BC边上,且EF垂直平分对角线AC,垂足为O.求证:四边形AECF为菱形.
如图,在?ABCD中,点E,F分别在AD,BC边上,且EF垂直平分对角线AC,垂足为O.求证:四边形AECF为菱形. 如图,C,D两点是双曲线y=
如图,C,D两点是双曲线y=