题目内容
 如图,已知点A、F、C、D在同一条直线上,AC=DF,BC∥EF,只需补充一个条件,就可得△ABC≌△DEF.则下列条件中不符合要求的是( )
如图,已知点A、F、C、D在同一条直线上,AC=DF,BC∥EF,只需补充一个条件,就可得△ABC≌△DEF.则下列条件中不符合要求的是( )| A、AB=DE |
| B、BC=EF |
| C、∠B=∠E |
| D、AB∥DE |
考点:全等三角形的判定
专题:常规题型
分析:根据平行线的性质由BC∥EF得到∠ACB=∠DFE,加上AC=DF,则根据全等三角形的判定方法分别对四个选项中的条件进行判断,看是否符合要求.
解答:解:∵BC∥EF,
∴∠ACB=∠DFE,
而AC=DF,
∴当添加AB=DE时,不能判断△ABC≌△DEF;
当添加BC=EF时,可根据“SAS”判断△ABC≌△DEF;
当添加∠B=∠E时,可根据“AAS”判断△ABC≌△DEF;
当添加AB∥DE时,则∠A=∠D,可根据“ASA”判断△ABC≌△DEF.
故选A.
∴∠ACB=∠DFE,
而AC=DF,
∴当添加AB=DE时,不能判断△ABC≌△DEF;
当添加BC=EF时,可根据“SAS”判断△ABC≌△DEF;
当添加∠B=∠E时,可根据“AAS”判断△ABC≌△DEF;
当添加AB∥DE时,则∠A=∠D,可根据“ASA”判断△ABC≌△DEF.
故选A.
点评:本题考查了全等三角形的判定:全等三角形的5种判定方法中,选用哪一种方法,取决于题目中的已知条件,若已知两边对应相等,则找它们的夹角或第三边;若已知两角对应相等,则必须再找一组对边对应相等,且要是两角的夹边,若已知一边一角,则找另一组角,或找这个角的另一组对应邻边.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
| A、第一次右拐60°,第二次左拐120° |
| B、第一次左拐60°,第二次右60° |
| C、第一次左拐60°,第二次左拐120° |
| D、第一次右拐60°,第二次右拐60° |
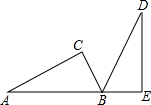 如图,将一个直角三角板ACB(∠C=90°)绕60°角的顶点B顺时针旋转,使得点C旋转到AB的延长线上的点E处,请解答下列问题:
如图,将一个直角三角板ACB(∠C=90°)绕60°角的顶点B顺时针旋转,使得点C旋转到AB的延长线上的点E处,请解答下列问题: 如图,在△ABC中,AB=AC,AD⊥BC于点D,且AD=
如图,在△ABC中,AB=AC,AD⊥BC于点D,且AD= 如图,在⊙O中,半径OA⊥弦BC,点E为垂足,点D在优弧上.
如图,在⊙O中,半径OA⊥弦BC,点E为垂足,点D在优弧上.