题目内容
 如图,已知反比例函数y1=
如图,已知反比例函数y1=| k1 |
| x |
(1)求反比例函数与一次函数的表达式;
(2)请直接写出B点的坐标,并指出当x为何值时,反比例函数y1的值小于一次函数y2的值.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据△OAC的面积为1,得出k1,即可得出反比例函数的表达式;再由tan∠AOC=2,设出点A坐标,即可求出A点坐标,从而得出一次函数的表达式;
(2)由图象即可得出B点的坐标,以及x的取值范围.
(2)由图象即可得出B点的坐标,以及x的取值范围.
解答: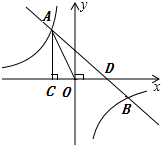 解:(1)∵点A在y1=
解:(1)∵点A在y1=
的图象上,S△ACO=1,
∴|k1|=2×1=2,
又∵k1<0,
∴k1=-2.
∴反比例函数的表达式为y1=-
.
设点A(a,-
),a<0,
∵在Rt△AOC中,tan∠AOC=
=2,
∴
=2,
∵a<0,
∴a=-1.
∴A(-1,2).
∵点A(-1,2)在y2=k2x+1上,
∴2=-k2+1,
∴k2=-1.
∴一次函数的表达式为y2=-x+1.
(2)点B坐标为(2,-1),
观察图象可知,当x<-1或0<x<2时,
反比例函数y1的值小于一次函数y2的值.
 解:(1)∵点A在y1=
解:(1)∵点A在y1=| k1 |
| x |
∴|k1|=2×1=2,
又∵k1<0,
∴k1=-2.
∴反比例函数的表达式为y1=-
| 2 |
| x |
设点A(a,-
| 2 |
| a |
∵在Rt△AOC中,tan∠AOC=
| AC |
| OC |
∴
-
| ||
| -a |
∵a<0,
∴a=-1.
∴A(-1,2).
∵点A(-1,2)在y2=k2x+1上,
∴2=-k2+1,
∴k2=-1.
∴一次函数的表达式为y2=-x+1.
(2)点B坐标为(2,-1),
观察图象可知,当x<-1或0<x<2时,
反比例函数y1的值小于一次函数y2的值.
点评:本题考查了一次函数和反比例函数的交点问题,以及用待定系数法求反比例函数和一次函数的解析式,是基础知识要熟练掌握.

练习册系列答案
相关题目
-9的绝对值是( )
| A、9 | ||
| B、-9 | ||
| C、±9 | ||
D、
|
二次函数y=ax2+bx+c的自变量x与函数y的对应值如下表,可判断二次函数的图象与x轴( )
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | 1 | -2 | -3 | -2 | … |
| A、只有一个公共点 |
| B、有两个交点,且它们分别在y轴两侧 |
| C、有两个交点,且它们均在y轴同侧 |
| D、无公共点 |
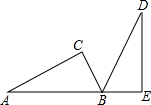 如图,将一个直角三角板ACB(∠C=90°)绕60°角的顶点B顺时针旋转,使得点C旋转到AB的延长线上的点E处,请解答下列问题:
如图,将一个直角三角板ACB(∠C=90°)绕60°角的顶点B顺时针旋转,使得点C旋转到AB的延长线上的点E处,请解答下列问题: 如图,在⊙O中,半径OA⊥弦BC,点E为垂足,点D在优弧上.
如图,在⊙O中,半径OA⊥弦BC,点E为垂足,点D在优弧上.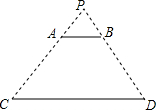 如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=5m,点P到CD的距离是3m,则AB与CD的距离是( )m.
如图,光源P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2m,CD=5m,点P到CD的距离是3m,则AB与CD的距离是( )m.