题目内容

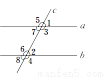
(1)如图所示,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.

(2)自由下落的物体的高度h(米)与下落时间t(秒)的关系为h=4.9t2.有一学生不慎把一个玻璃杯从19.6米高的楼上掉下,刚好另有一学生站在与下落的玻璃杯同一直线的地面上,在玻璃杯下落的同时楼上的学生惊叫一声.则这时楼下的学生能躲开吗?(学生反应时间为1秒,声音的传播速度为340米/秒)

(1)∠2 =50°;(2)楼下的学生能躲开,理由见解析. 【解析】试题分析: (1) 由两直线平行判断同位角相等和同旁内角互补，由角平分线的定义和对顶角相等，得到结论． (2)求出玻璃杯下落的时间，以及声音传到楼下的学生的时间，两者比较大小关系即可． 试题解析: (1)∵AB∥CD, ∴∠ABC=∠1=65°,∠ABD+∠BDC=180°. ∵BC平分∠ABD...
练习册系列答案
相关题目

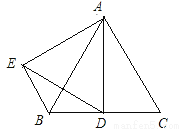
如图：△ABC和△ADE是等边三角形，AD是BC边上的中线．求证：BE=BD．

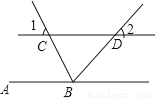
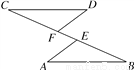
证明见解析. 【解析】试题分析：根据等边三角形三线合一的性质可得AD为∠BAC的角平分线，根据等边三角形各内角为60°即可求得∠BAE=∠BAD=30°，进而证明△ABE≌△ABD，得BE=BD． 试题解析：（方法1）证明：∵△ABC和△ADE都是等边三角形 ∴∠DAE=∠BAC=60°∴∠EAB=∠DAC ∵AE=AD，AB=AC ∴△ABE≌△ACD（SAS） ... 复制答案 考点分析： 相关试题推荐

如图，点C，F，E，B在一条直线上，∠CFD＝∠BEA，CE＝BF，DF＝AE，写出CD与AB之间的关系，并证明你的结论．

查看答案

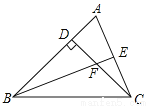
如图，在△ABC中，CD是AB边上高，BE为角平分线，若∠BFC=113°，求∠BCF的度数．

查看答案

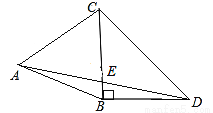
如图，△ABC是等边三角形，∠CBD=90°，BD=BC，连接AD交BC于点E，则∠AEC的度数是_________．

查看答案

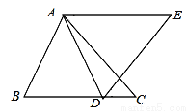
如图，在△ABC中，点D在BC上且AB=AD，AC=AE，∠BAD=∠CAE，DE=12，CD=4，则BD=_________．

查看答案

等腰三角形的一个内角为80°，则顶角的度数是_________．

查看答案 试题属性
  • 题型：解答题
  • 难度：中等
Copyright @ 2008-2013 满分5 学习网 ManFen5.COM. All Rights Reserved.答案无忧

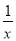下列方程：①x－2＝；②3x＝11；③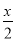＝5x－1；④y2－4y＝3；⑤x＋2y＝1.其中是一元一次方程的是________．(填序号)

②③ 【解析】因为一元一次方程满足的条件是: ①是整式方程,分母中不含未知数,②只含有一个未知数,③未知数的最高指数是1,故答案为: ②③.

多项式1+2xy﹣3xy2的次数及最高次项的系数分别是（ ）

A. 3，﹣3 B. 2，﹣3 C. 5，﹣3 D. 2，3

A 【解析】试题分析：多项式的次数看每一个单项式的最高次数，则次数为3次，系数为－3.

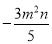－a2b的系数是________，次数是________；

26x3y2的系数是________，次数是________；

的系数是________，次数是________．

-1 3 5 3 【解析】单项式的系数是指单项式中的数字因数，次数是所有字母指数之和，故－a2b的系数是-1，次数是2+1=3；26x3y2的系数是26，次数是3+2=5； 的系数是，次数是2+1=3． 故答案为：-1，3； ，5； ，3.

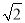同学们玩过“24点”游戏吗?现给你一个无理数,你再找3个有理数,使它们经过3次运算后结果为24.请你写出一个符合要求的等式:____.

×0+1+23=24 【解析】此题答案不唯一,符合要求的等式可以是×0+1+23=24,( )2+27- 5=24,( )4+25- 5=24等.

如图所示,直线a,b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°;④∠5+∠8=180°.其中能判断a∥b的条件是 (　　)

A. ①② B. ②④ C. ①③④ D. ①②③④

D 【解析】因为∠1=∠2, 所以a∥b(同位角相等,两直线平行); 因为∠3=∠6, 所以a∥b(内错角相等,两直线平行); 因为∠4=∠6,∠4+∠7=180°, 所以∠6+∠7=180°, 所以a∥b(同旁内角互补,两直线平行); 因为∠5=∠3,∠8=∠2,∠5+∠8=180°, 所以∠2+∠3=180°, 所以a∥b(同旁内角互...

如图，已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，下列4个结论：①abc＜0；②b＜a+c；③4a+2b+c＞0；④b2﹣4ac＞0其中正确结论的有（　　）

A. ①②③ B. ①②④ C. ①③④ D. ②③④

B 【解析】试题分析：由二次函数的图象开口向上可得a＞0，根据二次函数的图象与y轴交于正半轴知：c＞0，由对称轴直线x=2，可得出b与a异号，即b＜0，则abc＜0，故①正确； 把x=﹣1代入y=ax2+bx+c得：y=a﹣b+c，由函数图象可以看出当x=﹣1时，二次函数的值为正，即a﹣b+c＞0，则b＜a+c，故②选项正确； 把x=2代入y=ax2+bx+c得：y=4a+2b+...

用两个钉子就可以把木条钉在墙上，其依据是_________．

两点确定一条直线 【解析】根据直线的性质:两点确定一条直线,故答案为:两点确定一条直线.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网