题目内容
8.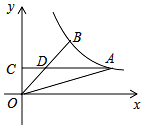 如图,A,B是反比例函数y=$\frac{k}{x}$图象上的两点,过点A作AC⊥y轴,垂足为C,AC交OB于点D.若D为OB的中点,△AOD的面积为6,则k的值为16.
如图,A,B是反比例函数y=$\frac{k}{x}$图象上的两点,过点A作AC⊥y轴,垂足为C,AC交OB于点D.若D为OB的中点,△AOD的面积为6,则k的值为16.
分析 先设点D坐标为(a,b),得出点B的坐标为(2a,2b),A的坐标为(4a,b),再根据△AOD的面积为6,列出关系式求得k的值.
解答 解:设点D坐标为(a,b),
∵点D为OB的中点,
∴点B的坐标为(2a,2b),
∴k=4ab,
又∵AC⊥y轴,A在反比例函数图象上,
∴A的坐标为(4a,b),
∴AD=4a-a=3a,
∵△AOD的面积为6,
∴$\frac{1}{2}$×3a×b=6,
∴ab=4,
∴k=4ab=4×4=16.
故答案为:16.
点评 本题主要考查了反比例函数系数k的几何意义,以及运用待定系数法求反比例函数解析式,根据△AOD的面积为6列出关系式是解题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
17.对抛物线y=-x2+2x-3,下列结论正确的是( )
| A. | 有最低点 | B. | 开口向上 | ||
| C. | 与y轴交点坐标是(0,3) | D. | 顶点坐标是(1,-2) |
18.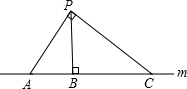 如图所示,P为直线m外一点,点A、B、C在直线m上,且PB⊥m,垂足为B,∠APC=90°,则下列说法错误的是( )
如图所示,P为直线m外一点,点A、B、C在直线m上,且PB⊥m,垂足为B,∠APC=90°,则下列说法错误的是( )
 如图所示,P为直线m外一点,点A、B、C在直线m上,且PB⊥m,垂足为B,∠APC=90°,则下列说法错误的是( )
如图所示,P为直线m外一点,点A、B、C在直线m上,且PB⊥m,垂足为B,∠APC=90°,则下列说法错误的是( )| A. | 线段PB的长度叫做点P到直线m的距离 | |
| B. | PA、PB、PC三条线段中,PB最短 | |
| C. | 线段PA的长度叫做点A到直线PC的距离 | |
| D. | 线段AC的长度等于点P到直线m的距离 |
 图中的四边形均是矩形,根据图形,写出一个正确的等式:
图中的四边形均是矩形,根据图形,写出一个正确的等式: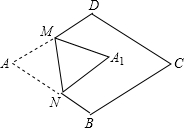 如图,在边长为2的菱形ABCD中,∠A=60°,M是边AD的中点,N是AB上一动点(不与A、B重合),将△AMN沿MN所在直线翻折得到△A1MN,连接A1C,画出点N从A到B的过程中A1的运动轨迹,A1C的最小值为$\sqrt{7}$-1.
如图,在边长为2的菱形ABCD中,∠A=60°,M是边AD的中点,N是AB上一动点(不与A、B重合),将△AMN沿MN所在直线翻折得到△A1MN,连接A1C,画出点N从A到B的过程中A1的运动轨迹,A1C的最小值为$\sqrt{7}$-1.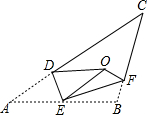 如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为=41°.
如图,将△ABC沿DE,EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=98°,则∠C的度数为=41°.