题目内容
16．若长为5cm，12cm，a cm的三条线段首尾顺次连接恰好围成一个直角三角形，则a的值是13或$\sqrt{119}$．分析 已知直角三角形的两边的长度求第三边，分两种情况，较大的边为直角边或斜边，然后根据勾股定理列方程解答．
解答 解：当边长为12cm的线段为直角边时，根据勾股定理得；52+122=a2，
解得；a=13，
边长为12cm的线段为斜边时，根据勾股定理得；52+a2=122，
解得：a=$\sqrt{119}$，
综上所述：若长为5cm，12cm，a cm的三条线段首尾顺次连接恰好围成一个直角三角形，则a的值是：13或$\sqrt{119}$，
故答案为：13或$\sqrt{119}$．
点评 本题考查了勾股定理，三角形的三边关系，注意分类思想在本题中的应用，不要漏解．
练习册系列答案
相关题目
6．
如图，已知S△ABC=12，AD平分∠BAC，且AD⊥BD于点D，则S△ADC的值是（ ）
如图，已知S△ABC=12，AD平分∠BAC，且AD⊥BD于点D，则S△ADC的值是（ ）| A． | 10 | B． | 8 | C． | 6 | D． | 4 |
4．
如图，在△ABC中，∠ACB=90°，AC=BC，点F在AB上，连接CF，AE⊥CF于E，BD垂直CF的延长线于点D．若AE=4cm，BD=2cm，则EF的长是（ ）
如图，在△ABC中，∠ACB=90°，AC=BC，点F在AB上，连接CF，AE⊥CF于E，BD垂直CF的延长线于点D．若AE=4cm，BD=2cm，则EF的长是（ ）| A． | $\frac{1}{3}$cm | B． | $\frac{2}{3}$cm | C． | 1cm | D． | $\frac{4}{3}$cm |
11．若一个正方形的面积为8，则这个正方形的边长为（ ）
| A． | 4 | B． | 2$\sqrt{2}$ | C． | $\sqrt{2}$ | D． | 8 |
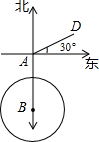如图所示，一艘轮船以20海里/时的速度由西向东航行，途中接到台风警报，台风正以40海里/时的速度由南向北移动，距台风20$\sqrt{2}$海里的圆形区域（包括边界）都属台风区．当轮船到A处时，测得台风中心移到位于点A正南方向B处，且AB=100海里．
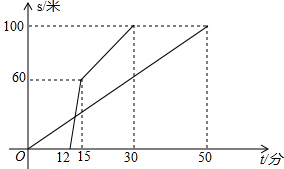在“龟兔赛跑”中，兔子输给乌龟极不服气，所以它约乌龟再赛一场，以雪耻前辱．在这次赛跑中乌龟提高了速度，兔子也全力以赴．但兔子在跑步过程中腿受伤了，速度也由此减慢了，乌龟一直匀速跑到最后．如图是乌龟和兔子跑步的路程S（米）与乌龟出发的时间t（分）之间的函数图象．根据图象提供的信息解决问题：