题目内容
5.直线y=$\frac{3}{2}$x+3与x轴,y轴所围成的三角形的面积为3.分析 先根据坐标轴上点的坐标特征求出直线与坐标轴的交点坐标,然后根据三角形面积公式求解.
解答 解:当x=0时,y=$\frac{3}{2}$x+3=3,则直线与y轴的交点坐标为(0,3),
当y=0时,$\frac{3}{2}$x+3=0,解得x=-2,则直线与x轴的交点坐标为(-2,0),
所以直线y=$\frac{3}{2}$x+3与x轴,y轴所围成的三角形的面积=$\frac{1}{2}$×3×2=3.
故答案为3.
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
相关题目
15.下列各式中,与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{15}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{1}{12}}$ |
13.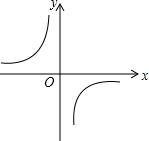 反比例函数y=$\frac{m}{x}$的图象如图所示,则下列结论正确的是( )
反比例函数y=$\frac{m}{x}$的图象如图所示,则下列结论正确的是( )
 反比例函数y=$\frac{m}{x}$的图象如图所示,则下列结论正确的是( )
反比例函数y=$\frac{m}{x}$的图象如图所示,则下列结论正确的是( )| A. | 常数m<1 | |
| B. | y随x的增大而增大 | |
| C. | 若A(-1,h),B(2,k)在图象上,则h<k | |
| D. | 若P(-x,y)在图象上,则P′(x,-y)也在图象上 |
20.下列函数中,是一次函数但不是正比例函数的是( )
| A. | y=2x | B. | y=$\frac{1}{x}$+2 | C. | y=$\frac{1}{3}$-$\frac{1}{2}$x | D. | y=2x2-1 |
10.已知点P(x.y)在x轴上方,且|x|=2,|y|=3,则点P的坐标是( )
| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (2,3)或(-2,3) |
17.“端午节”前夕,为保证绿色食品供应,我市准备组织20辆汽车到外地购进黄瓜、豆角、西红柿三种蔬菜共100吨.按计划20辆车都要装运,每辆汽车只能装运同一种蔬菜且必须装满.根据表格提供的信息,解答下列问题.
(1)设装运黄瓜的车辆数为x,装运豆角的车辆数为y,求y与x之间的函数关系式;
(2)如果装运黄瓜的车辆数不少于5辆,装运豆角的车辆数不少于4辆,那么,车辆的安排有几种方案?并写出每种安排方案?
(3)在(2)的条件下,应采用哪种方案才能使总运费W最少?并求出最少总运费W.
| 蔬菜种类 | 黄瓜 | 豆角 | 西红柿 |
| 每辆汽车运载量/吨 | 6 | 5 | 4 |
| 每吨所需运费/元/吨 | 120 | 160 | 180 |
(2)如果装运黄瓜的车辆数不少于5辆,装运豆角的车辆数不少于4辆,那么,车辆的安排有几种方案?并写出每种安排方案?
(3)在(2)的条件下,应采用哪种方案才能使总运费W最少?并求出最少总运费W.
 如图,在?ABCD中,对角线AC与BD相交于点O,则图中共有4对全等三角形.
如图,在?ABCD中,对角线AC与BD相交于点O,则图中共有4对全等三角形.