题目内容
20．
如图，在⊙O中，$\widehat{AB}$=$\widehat{AC}$，AB=2，则AC=2．
分析 由于在⊙O中，$\widehat{AB}$=$\widehat{AC}$，AB=2，根据圆心角、弧、弦的关系定理的推论可得AC=AB=2．
解答 解：∵在⊙O中，$\widehat{AB}$=$\widehat{AC}$，AB=2，
∴AC=AB=2．
故答案为2．
点评 本题考查了圆心角、弧、弦的关系定理的推论：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．注意：同一条弦对应两条弧，其中一条是优弧，一条是劣弧，而在本推论中的“弧”是指同为优弧或劣弧．
练习册系列答案
相关题目
有理数a、b、c在数轴上的对应点如图所示，化简代数式|2a-b|+3|a+b|-|4c-a|=-4a-2b-4c．
如图，已知l1∥l2∥l3，若$\frac{AB}{BC}$=$\frac{2}{3}$，DE=6，则EF=9．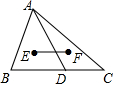
如图，在△ABC中，点D是BC上一点，E、F分别是△ABD、△ACD的重心，若BC=6，则线段EF的长为2．
12．
如图，某同学把一块三角形玻璃打碎了，现要去买一块大小形状完全相同的玻璃，那么最省事的办法是（ ）
如图，某同学把一块三角形玻璃打碎了，现要去买一块大小形状完全相同的玻璃，那么最省事的办法是（ ）| A． | 带①和②去 | B． | 带①去 | C． | 带②去 | D． | 带③去 |