题目内容
20. 如图,AE是△BAC的平分线,ED⊥AB于E,EF⊥AC于F,S△ABC=9,DE=2,AB=4,则AC的长为5.
如图,AE是△BAC的平分线,ED⊥AB于E,EF⊥AC于F,S△ABC=9,DE=2,AB=4,则AC的长为5.
分析 根据角平分线性质求出DE=EF=2,根据三角形面积公式求出即可.
解答 解:∵AE是∠BAC的平分线,ED⊥AB于E,EF⊥AC于F,DE=2,
∴EF=DE=2,
∵S△ABC=9,DE=2,AB=4,
∴S△ABC=$\frac{1}{2}×4×2+\frac{1}{2}×AC×2$=9,
解得:AC=5,
故答案为:5.
点评 本题考查了角平分线性质和三角形的面积,能根据角平分线性质得出DE=EF是解此题的关键.

练习册系列答案
相关题目
8.已知(ab+6)2与|4-2a|的值互为相反数,那么(a+b)2016的值等于( )
| A. | 2016 | B. | 1 | C. | -1 | D. | -2016 |
9.若分式$\frac{{x}^{2}-1}{x+1}$的值为零,那么x的值为( )
| A. | x=1或x=-1 | B. | x=-1 | C. | x=1 | D. | x=0 |
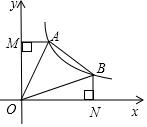 如图,直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N,现有以下结论:
如图,直线y=-x+b(b>0)与双曲线y=$\frac{k}{x}$(x>0)交于A、B两点,连接OA、OB,AM⊥y轴于M,BN⊥x轴于N,现有以下结论: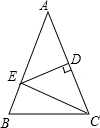 如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.
如图,△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC.