题目内容
11．函数y=$\frac{x}{x+3}$+（x-3）-2中自变量x的取值范围是x≠±3．分析 根据分式的分母不能为零，负整数指数的底数不能为零，可得不等式组，根据解不等式组，可得答案．
解答 解：由y=$\frac{x}{x+3}$+（x-3）-2有意义，得
$\left\{\begin{array}{l}{x+3≠0}\\{x-3≠0}\end{array}\right.$．
解得x≠-3，x≠3．
故答案为：x≠±3．
点评 本题考查了函数自变量的取值范围，分式的分母不能为零，负整数指数的底数不能为零．
练习册系列答案
浙江新课程三维目标测评课时特训系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
1．下列关于向量的等式中，正确的是（ ）
| A． | $\overrightarrow{AB}$=$\overrightarrow{BA}$ | B． | $\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{CA}$ | C． | $\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{b}$+$\overrightarrow{a}$ | D． | $\overrightarrow{a}$+（-$\overrightarrow{a}$）=$\overrightarrow{0}$ |
如图∠A=40°，∠ABD=∠D=∠F=90°，AG⊥GF于G，求∠E的度数．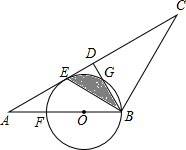
已知，如图，在△ABC中，AB=BC，D是AC的中点，BE平分∠ABD交AC于点E，点O是AB边上一点，⊙O过B、E两点，交BD于点G，交AB于点F．
6．
如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于E，分别连接AD、BC，已知∠D=65°，则∠OCD=（ ）
如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于E，分别连接AD、BC，已知∠D=65°，则∠OCD=（ ）| A． | 30° | B． | 35° | C． | 40° | D． | 45° |
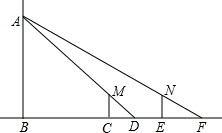如图，小明晚上由路灯A下的点B处走到点C处时，测得自身影子CD的长为1米，他继续往前走3米到达点E处（即CE=3米），测得自己影子EF的长为2米，已知小明的身高是1.5米，那么路灯A的高度AB是（ ）