题目内容
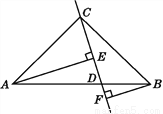
如图:在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.试判断AC与BC的位置关系,并说明理由.
练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
题目内容
如图:在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.试判断AC与BC的位置关系,并说明理由.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案