题目内容
18.已知关于x的方程kx2+(1-k)x-1=0,有下列说法:①当k=0时,方程无解;
②当k=1时,方程有一个实数解;
③当k=-1时,方程有两个相等的实数解;
④此方程总有实数解.
其中错误的是①②.
分析 当k≠0时,找出b2-4ac=(1+k)2.①当k=0时,找出方程,解方程发现方程有一个实数根,从而判断①不正确;②将k=1代入b2-4ac=(1+k)2中,得出△>0,由此得出②不正确;③将k=-1代入b2-4ac=(1+k)2中,得出△=0,由此得出③正确;④结合①可知当k=0时,方程有实数根,当k≠0时,由b2-4ac=(1+k)2≥0可得出方程有实数根,从而得出④正确,结合上面所述即可得出结论.
解答 解:当k≠0时,b2-4ac=(1-k)2+4k=(1+k)2.
①当k=0时,原方程为x-1=0,
解得:x=1,①不正确;
②当k=1时,b2-4ac=(1+k)2=4>0,
∴方程有两个不相等的实数根,②不正确;
③当k=-1时,b2-4ac=(1+k)2=0,
∴方程有两个相等的实数根,③正确;
④当k=0时,同①方程有解;
当k≠0时,b2-4ac=(1+k)2≥0,
方程有解.
∴④正确.
故答案为:①②.
点评 本题考查了根的判别式,解题的关键是找出b2-4ac=(1+k)2.本题属于基础题,难度不大,解决该题型题目时,根据根的判别式得出方程实数根的个数是关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
8.在2,$\frac{1}{2}$,0,-2四个数中,最大的数是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | 0 | D. | -2 |
6.下列方程中2x-3y=1,x+y2=5,$\frac{1}{x}$-$\frac{1}{y}$=2,$\frac{1}{3}$x-$\frac{1}{2}$y=z,不是二元一次方程的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.下列各数中,最小的数是( )
| A. | 3-2 | B. | $\frac{2}{5}$ | C. | |-$\frac{1}{7}$| | D. | $\sqrt{2}$ |
7.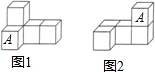 如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图(1)变到图(2),不改变的是( )
如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图(1)变到图(2),不改变的是( )
 如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图(1)变到图(2),不改变的是( )
如图,小明用6个相同的小正方体搭成的立体图形研究几何体的三视图的变化情况,若由图(1)变到图(2),不改变的是( )| A. | 主视图 | B. | 主视图和左视图 | C. | 主视图和俯视图 | D. | 左视图和俯视图 |
8.在方程(k2-4)x2+(2-3k)x+(k+1)y+3k=0中,若此方程为二元一次方程,则k值为( )
| A. | -2 | B. | 2或-2 | C. | 2 | D. | 以上答案都不对 |
 如图,投影线的方向如箭头所示.画出下列图中几何体的正投影.
如图,投影线的方向如箭头所示.画出下列图中几何体的正投影.