题目内容
 如图,△ABC中,AB=6,AC=8,BC=10,
如图,△ABC中,AB=6,AC=8,BC=10,(1)证明:△ABC是直角三角形.
(2)若AD⊥BC,垂足为D,求AD的长.
考点:勾股定理的逆定理
专题:
分析:(1)利用勾股定理的逆定理即可证明;
(2)根据三角形的面积公式可得
BC•AD=
AB•AC,那么AD=
,将数值代入计算即可.
(2)根据三角形的面积公式可得
| 1 |
| 2 |
| 1 |
| 2 |
| AB•AC |
| BC |
解答:(1)证明:在△ABC中,∵AB2+AC2=62+82=100=102,
∴AB2+AC2=BC2,
∴△ABC是直角三角形;
(2)∵△ABC的面积=
BC•AD=
AB•AC,
∴AD=
=
=4.8.
∴AB2+AC2=BC2,
∴△ABC是直角三角形;
(2)∵△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
| AB•AC |
| BC |
| 6×8 |
| 10 |
点评:本题考查了勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.同时考查了三角形的面积.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )| A、CM=DM | ||||
B、
| ||||
| C、∠ACD=∠ADC | ||||
| D、OM=BM |
下列各式是一元一次方程的是( )
| A、x+y=1 | ||
| B、x2+x=1 | ||
| C、2x+3=5-x | ||
D、
|
 如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
如图,直线a、b、c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )| A、一处 | B、两处 | C、三处 | D、四处 |
 如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D.
如图,⊙O的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙O于D.
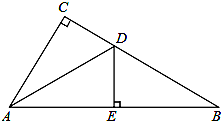 如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.若∠B=30°,CD=1,求BD的长.
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.若∠B=30°,CD=1,求BD的长.