��Ŀ����
9����-3��-2��-1��1��2��3���������У����ѡȡһ��������Ϊa������aʹ����x�IJ���ʽ��$\left\{\begin{array}{l}{\frac{1}{2}��2x+1����3}\\{x-a��0}\end{array}\right.$�⣬��ʹ����x�ķ�ʽ����$\frac{x}{x-1}$+$\frac{a+2}{1-x}$=3�������⣬��ô������������������������a��ֵ֮���ǣ�������| A�� | -3 | B�� | -2 | C�� | -1 | D�� | 0 |
���� �ɲ���ʽ����ȷ����a�ķ�Χ�������ʽ����ʹ���Ϊ����ȷ����a��ֵ�����֮�ͼ��ɣ�
��� �⣺����ʽ�������ã�$\left\{\begin{array}{l}{x��2.5}\\{x��a}\end{array}\right.$��
�ɲ���ʽ���⣬�õ�a��2.5��
��a��ֵ����Ϊ-3��-2��-1��1��2��
��a=-3ʱ����ʽ����Ϊ$\frac{x}{x-1}$+$\frac{1}{x-1}$=3��
��ã�x=2��
������x=2�Ƿ�ʽ���̵Ľ⣻
��a=-2ʱ����ʽ����Ϊ$\frac{x}{x-1}$=3��
��ã�x=1.5��
������x=1.5�Ƿ�ʽ���̵Ľ⣬���������⣻
��a=-1ʱ����ʽ����Ϊ$\frac{x}{x-1}$-$\frac{1}{x-1}$=3��
��ã�x=1��
������x=1����������ʽ�����⣻
��a=1ʱ����ʽ����Ϊ$\frac{x}{x-1}$+$\frac{3}{1-x}$=3��
��ã�x=0��
������x=0�Ƿ�ʽ���̵Ľ⣻
��a=2ʱ����ʽ����Ϊ$\frac{x}{x-1}$+$\frac{4}{1-x}$=3��
��ã�x=-$\frac{1}{2}$��
������x=-$\frac{1}{2}$�Ƿ�ʽ���̵Ľ⣬���������⣬
���ϣ���������a��ֵΪ-3��1��֮��Ϊ-2��
��ѡB
���� ���⿼���˷�ʽ���̵Ľ⣬�Լ���һԪһ�β���ʽ�飬�����������㷨���ǽⱾ��Ĺؼ���

 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�| A�� | -10 | B�� | 10 | C�� | -20 | D�� | 20 |
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | 2 |

| A�� | �٢� | B�� | �٢� | C�� | �٢� | D�� | �ۢ� |
 ��ͼ���ڡ�ABC�У�AB=5��AC=3��BC=4��D��BC����һ���㣬BE��AD�������ӳ����ڵ�E��EF��AC�������ӳ����ڵ�F����AF�����ֵΪ4��
��ͼ���ڡ�ABC�У�AB=5��AC=3��BC=4��D��BC����һ���㣬BE��AD�������ӳ����ڵ�E��EF��AC�������ӳ����ڵ�F����AF�����ֵΪ4��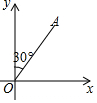 ij�ۿ����ϱ��������ϵĵ�O���ס������ҿ���ͬʱ�뿪�ۿڣ����е��ٶȶ���40m/min��������15min����A���ҿ�����20min����B����A��B������ֱ�߾���Ϊ1000m����֪�������ű�ƫ��30��ķ����У�
ij�ۿ����ϱ��������ϵĵ�O���ס������ҿ���ͬʱ�뿪�ۿڣ����е��ٶȶ���40m/min��������15min����A���ҿ�����20min����B����A��B������ֱ�߾���Ϊ1000m����֪�������ű�ƫ��30��ķ����У�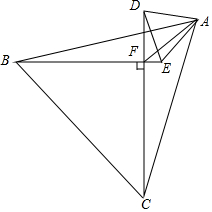 ����ABC������ADE��BE��CD��FΪ���㣬AF=1����S��ABC+S��ADE��
����ABC������ADE��BE��CD��FΪ���㣬AF=1����S��ABC+S��ADE��