题目内容
19.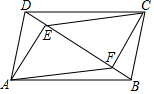 如图,在?ABCD中,BD是它的一条对角线,过A、C两点分别作AE⊥BD,CF⊥BD,E、F为垂足.求证:四边形AFCE是平行四边形.
如图,在?ABCD中,BD是它的一条对角线,过A、C两点分别作AE⊥BD,CF⊥BD,E、F为垂足.求证:四边形AFCE是平行四边形.
分析 连接AC交BD于点O,由平行四边形的性质可证明△AED≌△CFB,则可求得DE=BF,从而可求得OE=OF,可证得结论.
解答 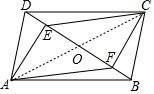 证明:
证明:
连接AC交BD于点O,
∵四边形ABCD为平行四边形,
∴OA=OC,OD=OB,AD∥BC,AD=BC,
∴∠ADE=∠CBF,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB,
在△AED和△CFB中
$\left\{\begin{array}{l}{∠AED=∠CFB}\\{∠ADE=∠CBF}\\{AD=BC}\end{array}\right.$
∴△AED≌△CFB(AAS),
∴DE=BF,
∴OD-DE=OB-BF,即OE=OF,
∴四边形AFCE是平行四边形.
点评 本题主要考查平行四边形的判定和性质,掌握平行四边形的判定和性质是解题的关键,即①两组对边分别平行四边形?平行四边形,②两组对边分别相等的四边形?平行四边形,③一组对边平行且相等的四边形?平行四边形,④两组对角分别相等的四边形?平行四边形,⑤对角线互相平分的四边形?平行四边形.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 在数学课上,老师提出如下问题:
在数学课上,老师提出如下问题: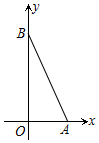 在平面直角坐标系中,点A(1,0)、B(0,3),以AB为边在第一象限作等腰直角△ABC,则点C的坐标为(3,4)、(4,1)、(2,2).
在平面直角坐标系中,点A(1,0)、B(0,3),以AB为边在第一象限作等腰直角△ABC,则点C的坐标为(3,4)、(4,1)、(2,2). 如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=100°,∠ACF=20°,求∠FEC的度数.
如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=100°,∠ACF=20°,求∠FEC的度数.