题目内容
19．不等式组$\left\{\begin{array}{l}{x+3＞6}\\{2x-1＜10}\end{array}\right.$的正整数解的个数是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 此题可先根据一元一次不等式组解出x的取值，根据x是正整数解得出x的可能取值．
解答 解：$\left\{\begin{array}{l}{x+3＞6①}\\{2x-1＜10②}\end{array}\right.$，
由①得x＞3；
由②得x＜5.5；
由以上可得3＜x＜5.5，
∵x为正整数，
∴不等式组的正整数解是：4，5，个数是2．
故选：B．
点评 此题考查的是一元一次不等式组的解法，根据x的取值范围，求出x的正整数解即可．求不等式组的解集，应遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．
练习册系列答案
相关题目
9．下列语句中，是假命题的是（ ）
| A． | 所有的实数都可用数轴上的点表示 | B． | 等角的补角相等 | ||
| C． | 互补的两个角是邻补角 | D． | 垂线段最短 |
10．三角形DEF是由三角形ABC平移得到的，点A（-1，-4）的对应点为D（1，-1），则点B（1，1）的对应点E，点C（-1，4）的对应点F的坐标分别为（ ）
| A． | （2，2），（3，4） | B． | （3，4），（2，-2） | C． | （-2，2），（1，7） | D． | （3，4），（1，7） |
7．
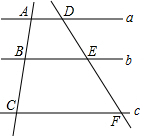如图，已知a∥b∥c，AC=6，AB=2，EF=5，则DF的值为（ ）
如图，已知a∥b∥c，AC=6，AB=2，EF=5，则DF的值为（ ）| A． | $\frac{5}{3}$ | B． | $\frac{5}{2}$ | C． | $\frac{10}{3}$ | D． | $\frac{15}{2}$ |
14．下列定理的逆命题为假命题的是（ ）
| A． | 两直线平行，内错角相等 | |
| B． | 直角三角形的两锐角互余 | |
| C． | 角平分线上的点到角两边的距离相等 | |
| D． | 对顶角相等 |
11．如果关于x的不等式组$\left\{\begin{array}{l}x＞a+2\\ x＜3a-2\end{array}\right.$无解，则a的取值范围是（ ）
| A． | a＜2 | B． | a＞2 | C． | a≥2 | D． | a≤2 |
8．
如图，在?ABCD中，AC与BD交于点O，下列说法正确的是（ ）
如图，在?ABCD中，AC与BD交于点O，下列说法正确的是（ ）| A． | AC=BD | B． | AC⊥BD | C． | AO=CO | D． | AB=BC |
9．用配方法解方程x2-2x-3=0，原方程应变形为（ ）
| A． | （x-1）2=2 | B． | （x+1）2=4 | C． | （x-1）2=4 | D． | （x+1）2=2 |