题目内容
在圆内接四边形ABCD中,若∠A:∠B:∠C=1:2:5,则∠B的度数是( )
| A、30° | B、45° |
| C、60° | D、120° |
考点:圆内接四边形的性质
专题:
分析:先根据在圆内接四边形ABCD中∠A:∠B:∠C=1:2:5,设∠A=x,则∠B=2x,∠C=5x,再根据圆内接四边形的对角互补求出x的值,进而可得出结论.
解答:解:∵圆内接四边形ABCD中∠A:∠B:∠C=1:2:5,设∠A=x,则∠B=2x,∠C=5x,
∵∠A+∠C=180°,即x+5x=180°,解得x=30°,
∴2x=60°.
故选C.
∵∠A+∠C=180°,即x+5x=180°,解得x=30°,
∴2x=60°.
故选C.
点评:本题考查的是圆内接四边形的性质,熟知圆内接四边形的对角互补是解答此题的关键.

练习册系列答案
相关题目
已知:点A,B,C为同一直线上,M,N分别是线段AB,BC的中点,AB=16cm,BC=6cm,则MN的长是( )cm.
| A、8 | B、11 |
| C、5或11 | D、8或11 |
下列各图不是正方体展开图的是( )
A、 |
B、 |
C、 |
D、 |
要反映定安县2014年各月份降雨量的变化情况,应选择( )统计图.
| A、条形 | B、折线 |
| C、扇形 | D、不能确定 |
一个矩形宽为1(宽<长),剪去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在数轴上表示满足不等式组
的x值的公共部分,正确的是( )
|
A、 |
B、 |
C、 |
D、 |
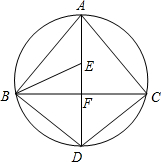 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD、CD.
如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD、CD. 如图所示,在直角△ABC中,已知∠C=90°,AB=10cm,BC=8cm,AC=6cm,点P从点A出发以3cm/s的速度经过点B向点C运动,同时,点Q从点B出发以2cm/s的速度向点C运动,设运动时间为t(s).
如图所示,在直角△ABC中,已知∠C=90°,AB=10cm,BC=8cm,AC=6cm,点P从点A出发以3cm/s的速度经过点B向点C运动,同时,点Q从点B出发以2cm/s的速度向点C运动,设运动时间为t(s). 如图所示,线段FC⊥AB于点C,且AC=FC,若AD⊥BF叫FC与点E,求证:CE=CB.
如图所示,线段FC⊥AB于点C,且AC=FC,若AD⊥BF叫FC与点E,求证:CE=CB.