题目内容
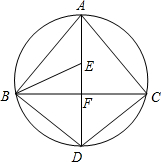 如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD、CD.
如图,AD为△ABC外接圆的直径,AD⊥BC,垂足为点F,∠ABC的平分线交AD于点E,连接BD、CD.求证:点B、E、C在以点D为圆心,BD为半径的圆上.
考点:圆周角定理,圆心角、弧、弦的关系
专题:证明题
分析:根据垂径定理,由AD⊥BC,
=
,则BD=CD,∠3=∠4,再由∠ABC的平分线交AD于点E得∠2=∠ABE,根据三角形外角性质有∠1=∠4+∠ABE,所以∠1=∠2+∠3,则根据等腰三角形的判定得DB=DE,于是DB=DE=DC,然后根据点与圆的关系得点B、E、C在以点D为圆心,BD为半径的圆上.
 |
| BD |
 |
| CD |
解答:证明: ∵AD为△ABC外接圆的直径,AD⊥BC,
∵AD为△ABC外接圆的直径,AD⊥BC,
∴
=
,
∴BD=CD,∠3=∠4,
∵∠ABC的平分线交AD于点E,
∴∠2=∠ABE,
∵∠1=∠4+∠ABE,
∴∠1=∠2+∠3,即∠1=∠DBE,
∴DB=DE,
∴DB=DE=DC,
∴点B、E、C在以点D为圆心,BD为半径的圆上.
 ∵AD为△ABC外接圆的直径,AD⊥BC,
∵AD为△ABC外接圆的直径,AD⊥BC,∴
 |
| BD |
 |
| CD |
∴BD=CD,∠3=∠4,
∵∠ABC的平分线交AD于点E,
∴∠2=∠ABE,
∵∠1=∠4+∠ABE,
∴∠1=∠2+∠3,即∠1=∠DBE,
∴DB=DE,
∴DB=DE=DC,
∴点B、E、C在以点D为圆心,BD为半径的圆上.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了圆心角、弧、弦的关系.

练习册系列答案
相关题目
数轴上的点A到原点的距离是8,则点A表示的数为( )
| A、8 | B、4或-4 |
| C、8或-8 | D、4 |
在圆内接四边形ABCD中,若∠A:∠B:∠C=1:2:5,则∠B的度数是( )
| A、30° | B、45° |
| C、60° | D、120° |




 二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论: 如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.
如图,抛物线y=mx2-2mx-3m(m>0)与x轴交于A、B两点,与y轴交于C点.