Question

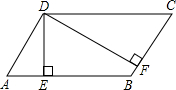如图所示，平行四边形ABCD中，DE⊥AB，DF⊥BC，垂足分别为EF，EDF=60°，CF=3cm，AE=2cm，求?ABCD的周长．

Answer 1

考点：平行四边形的性质

专题：

分析：首先根据DE⊥AB，DF⊥BC，∠EDF=60°，可求得∠B的度数，然后根据平行四边形的性质可求得∠A和∠C的度数，根据CF和AE的长度，求出AD和CD的长度，继而求得平行四边形ABCD的周长，

解答：解：∵DE⊥AB，DF⊥BC，∠EDF=60°，
∴∠B=120°，
∵四边形ABCD为平行四边形，
∴AB∥CD，
∴∠A=∠C=180°-120°=60°，
∴在Rt△DAE和Rt△DFC中，∠ADE=∠CDF=30°，
∵AE=2，CF=3，
∴AD=2AE=4，DC=2CF=6，
则ABCD的周长为20cm．

点评：此题考查了平行四边形的性质以及直角三角形的性质．此题难度不大，注意掌握数形结合思想的应用．